SHORTLINK: https://wolfr.am/yeganeh

The image above is in Scalable Vector Graphics (.SVG) format and can be zoomed without degradation and printed with high quality at any resolution. It can also be searched, indexed, scripted, compressed, and created and edited with any text editor. SVG is an open standard and is pure XML.
That's a great canvas for computationally generated art.
After reading this article I wished I'd have .SVG of the beautiful images. Another idea that crossed my mind was generalization of scattered cases listed there. Generalization is not only inference from special cases, but also the means to explore the infinite. Connecting the dots launches you to another dimension. I enjoy the art of Iranian mathematician Hamid Naderi Yeganeh who can make a stunning image from just circles and a math formula. Computation can be really fun to explore, especially when it can generate mysterious universes from a few simple rules. Many artists understand and use that in their creative process. I wanted to show how to create simple applications that would bring that joy of creative exploration into the hands of anyone, even very beginner programmers. You don't really have to know much to make beautiful things. And an eye-candy .SVG print would be a nice trophy.
Here is the result and below it I explain the mechanics. Click anywhere on the image to go the actual app interface and play. Remember computations take time (~ 10 seconds), please be patient. You can download your .SVG graphics via a right-click. Read below how the app works.
We start from a simple example given in the article and see how to program just the production of graphics for now. Later we design the app.
7,000 Circles (3)
According to Hamid Naderi Yeganeh the image below shows $7,000$ circles. For $k = 1,2,3,...,7000$, the center of $k-th$ circle is $(X(k), Y(k))$, and its radius is $R(K)$, where
$$X(k)=\sin \left(\frac{6 \pi k}{7000}\right) \left(1+\cos ^2\left(\frac{20 \pi k}{7000}\right)-\frac{1}{5} \cos ^2\left(\frac{16 \pi k}{7000}\right)\right)$$
$$Y(k)=\cos \left(\frac{6 \pi k}{7000}\right) \left(1+\cos ^2\left(\frac{20 \pi k}{7000}\right)-\frac{1}{5} \cos ^2\left(\frac{16 \pi k}{7000}\right)\right)$$
$$R(k)=\frac{1}{200}+\frac{1}{7} \cos ^2\left(\frac{28 \pi k}{7000}\right)+\frac{1}{7} \sin ^6\left(\frac{24 \pi k}{7000}\right)+\frac{1}{20} \cos ^4\left(\frac{84 \pi k}{7000}\right)$$
In Wolfram Language (WL) code these formulas become:
X[k_]:=Sin[(6? k)/7000](1+Cos[(20? k)/7000]^2-1/5 Cos[(16? k)/7000]^2);
Y[k_]:=Cos[(6? k)/7000](1+Cos[(20? k)/7000]^2-1/5 Cos[(16? k)/7000]^2);
R[k_]:=1/200+1/7 Cos[(28? k)/7000]^2+1/7 Sin[(24? k)/7000]^6+1/20 Cos[(84? k)/7000]^4;
To build the art in .SVG format we use (note I had to make up a procedure for coloring, it does not reflect what Dr. Yeganeh did):
p1=Graphics[{
Opacity[.3],
ParallelTable[{
LABColor[1,Cos[(2? k)/7000],Sin[(2? k)/7000]],
Circle[{X[k],Y[k]},R[k]]},
{k,1,7000,1.}]},
Background->Black]
Export["p1.svg", p1]

The mother formula
In a similar manner we can reproduce other examples here. But we should notice that formulas describing all of them look pretty similar. So instead of building each formula separately, we can generalize everything to a single formula and explore many more cases. While generalization is quite arbitrary, I suggest to play it close to the original (the copyable code is in attached notebook):

This might look messy, but the messy part is from necessity of safe-guiding an average user through settings that minimize production of nonsensical or mathematically failing images. Now, when we got the mother formula, it is time to design the app. But before we do that we must learn the basics.
Computational website in a nutshell
In ever-expanding vocabulary of the WL there are currently over 5000 "definitions" that are functions. Many are masterminds that drive an neural net or create a website. Let's create a simple example. This is how with a single function you can find semantic meaning of an image using convolutional neural networks:

And this is how with two essential functions (CloudDeploy and FromFunction) you can deploy (create) a dynamic computing website:
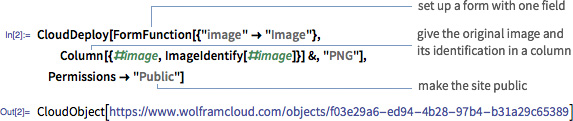
That's it, you are done. With some polish you get imageidentify.com, a website AI understanding images. There are quite a few similar ideas out there, but in WL you "say" that idea just "in a few words". That's the point behind a sophisticated language.
Per aspera ad astra
We will jump to a slightly larger code base. It is still pretty small for what it achieves. Good news is in WL all functions have completely spelled names and so WL tells a good story with the words you can read meaningfully.
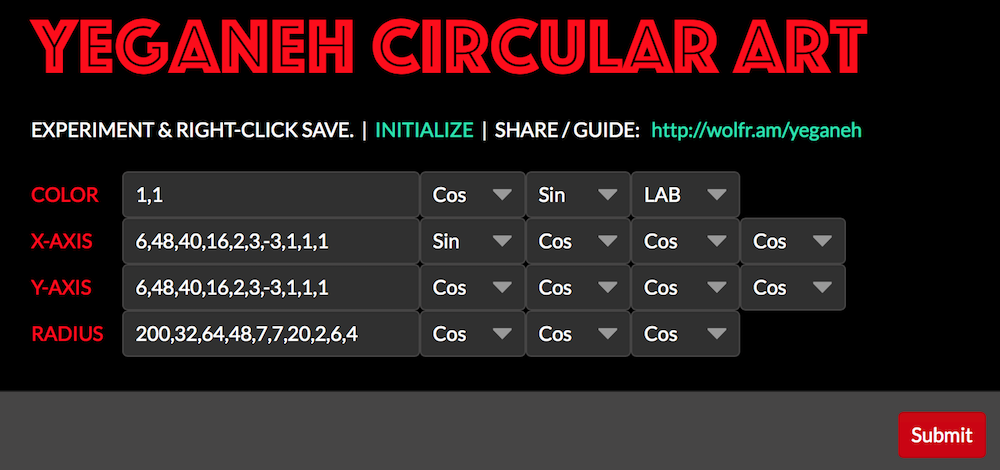
This is the end of the journey. I suggest you embark on another one by exploring the infinite Circular Yeganeh Universe.
CloudDeploy[
FormPage[
{"x1" -> <|"Input"->"1,1","Interpreter"->Restricted[DelimitedSequence[Restricted["Number", {-?, ?}]], {2}]|>,
"x2" -> <|"Input"->Cos,"Interpreter"->{"Cos"->Cos, "Sin"->Sin}|>,
"x3" -><|"Input"->Sin,"Interpreter"->{"Cos"->Cos, "Sin"->Sin}|>,
"x4" -> <|"Input"->LABColor,"Interpreter"->{"LAB"->LABColor, "LUV"->LUVColor,"XYZ"->XYZColor}|>,
"x5" -> <|"Input"->"6,48,40,16,2,3,-3,1,1,1","Interpreter"->Restricted[DelimitedSequence[Restricted["Number", {-?, ?}]], {10}]|>,
"x6" -> <|"Input"->Sin,"Interpreter"->{"Cos"->Cos, "Sin"->Sin}|>,
"x7" -> <|"Input"->Cos,"Interpreter"->{"Cos"->Cos, "Sin"->Sin}|>,
"x8" -> <|"Input"->Cos,"Interpreter"->{"Cos"->Cos, "Sin"->Sin}|>,
"x9"-> <|"Input"->Cos,"Interpreter"->{"Cos"->Cos, "Sin"->Sin}|>,
"x10" -> <|"Input"->"6,48,40,16,2,3,-3,1,1,1","Interpreter"->Restricted[DelimitedSequence[Restricted["Number", {-?, ?}]], {10}]|>,
"x11" -> <|"Input"->Cos,"Interpreter"->{"Cos"->Cos, "Sin"->Sin}|>,
"x12" -> <|"Input"->Cos,"Interpreter"->{"Cos"->Cos, "Sin"->Sin}|>,
"x13" -> <|"Input"->Cos,"Interpreter"->{"Cos"->Cos, "Sin"->Sin}|>,
"x14" -> <|"Input"->Cos,"Interpreter"->{"Cos"->Cos, "Sin"->Sin}|>,
"x15" -> <|"Input"->"200,32,64,48,7,7,20,2,6,4","Interpreter"->Restricted[DelimitedSequence[Restricted["Number", {-?, ?}]], {10}]|>,
"x16" -> <|"Input"->Cos,"Interpreter"->{"Cos"->Cos, "Sin"->Sin}|>,
"x17" -> <|"Input"->Cos,"Interpreter"->{"Cos"->Cos, "Sin"->Sin}|>,
"x18" -> <|"Input"->Cos,"Interpreter"->{"Cos"->Cos, "Sin"->Sin}|>},
Column[{
ExportForm[
Graphics[{
Opacity[.3],
Table[{
HU[k][#x2,#x3,#x4]@@#x1,
Circle[{
CO[k][#x6,#x7,#x8,#x9]@@#x5,
CO[k][#x11,#x12,#x13,#x14]@@#x10},
RA[k][#x16,#x17,#x18]@@#x15]},
{k,1,7000,1.}]},
ImageSize->1000,
Background->Black],
"SVG"],
Style["right-click on image to save", FontFamily->"Herculanum",Red,25]
}]&,
FormLayoutFunction -> Function[
Column[{
Style["yeganeh circular art",FontFamily->"Phosphate",60,Red],
Grid[{{
Style["EXPERIMENT & RIGHT-CLICK SAVE.",GrayLevel[7]],
Spacer[2],"|",Spacer[2],
Hyperlink["INITIALIZE","https://wolfr.am/yeganehAPP"],
Spacer[2],"|",Spacer[2],
Style["SHARE / GUIDE:",GrayLevel[7]],
Spacer[3],
Hyperlink["http://wolfr.am/StaffPicks","http://wolfr.am/StaffPicks"]
}},Spacings->{0, 0}],
Spacer[{1,5}],
Grid[
{{Style["COLOR",Red],Spacer[5],#["x1", "Control"], #["x2", "Control"], #["x3", "Control"],#["x4", "Control"]},
{Style["X-AXIS",Red],Spacer[5],#["x5", "Control"], #["x6", "Control"],#["x7", "Control"], #["x8", "Control"], #["x9", "Control"]},
{Style["Y-AXIS",Red],Spacer[5], #["x10", "Control"], #["x11", "Control"], #["x12", "Control"], #["x13", "Control"], #["x14", "Control"]},
{Style["RADIUS",Red],Spacer[5], #["x15", "Control"], #["x16", "Control"], #["x17", "Control"], #["x18", "Control"]}}
]
}]
],
FormTheme -> "Black"
],
"yeganeh",
Permissions->"Public"
]
 Attachments:
Attachments: