The popularity of the Hamilton musical is just nonstop. There are even some Hamilton goodies in WolframAlpha and the Wolfram Language:
EntityList[EntityClass["PopularCurve", "Hamilton"]]

GraphicsGrid[Partition[EntityValue[EntityList[EntityClass["PopularCurve", "Hamilton"]], "Image"], 4], ImageSize -> Large]

But before 2015, the only Hamilton I ever heard about regularly was...
"What's your name, man?"
"William Rowan Hamilton!"
Sir William was a young, scrappy, and hungry Irish mathematician and physicist for whom several objects in math and physics are named. His name also appears in some Wolfram Language symbols:
?*Hamilton*

These symbols have to do with Hamiltonian paths. A Hamiltonian path through a graph passes through each vertex exactly once. A Hamiltonian path that begins and ends at the same vertex is called a Hamiltonian cycle, and a graph is Hamiltonian if it contains a Hamiltonian cycle.
Personally I think the world is wide enough for both Hamiltons. So can we find a Hamiltonian graph in the Hamilton musical? It's time to take a shot.
To form a graph, we need vertices and edges. The 1, 2, 3, 4, 5, 6, 7, 8 characters represented by popular curves make natural vertices, since we have nice pictures for them. We just need to decide how to draw edges between them. One possibility would be to connect two characters if they're on stage at the same time, but that information isn't easy to get programmatically. We have the lyrics, thanks to the cast recording booklets and Genius. So let's draw a graph showing which characters talk about which other characters, drawing an edge from character $A$ to character $B$ if $A$ mentions $B$. Since the edges are directed edges, this will make it a bit harder for the graph to be Hamiltonian.
What comes next? A lot of text processing to get the lyrics into a structured form. For each character, we need the lines sung by that character. This requires handling compound instructions like "HAMILTON/BURR/LAURENS/ALL WOMEN (EXCEPT ELIZA)", realizing that "SCHUYLER SISTERS" includes Angelica, Eliza, #andPeggy, and correcting a few typos (notice the 4 ways of spelling "WASHINGTON"). 
That list of 66 "characters" of course contains duplicates, non-characters, and characters we don't care about. Many lines are sung by multiple characters, so I distributed those lines to each character they are assigned to, and finally collected all lines by character. I've attached the file to the bottom of this post.
linesbycharacter = Import["linesbycharacter.m"];
Here are the characters:
Sort[First /@ linesbycharacter]
{"ANGELICA", "BURR", "DOCTOR", "DOLLY", "ELIZA", "GEORGE", "HAMILTON", "JAMES", "JEFFERSON", "KING GEORGE", "LAFAYETTE",
"LAURENS", "LEE", "MADISON", "MARIA", "MARTHA", "MULLIGAN", "PEGGY", "PHILIP", "SEABURY", "WASHINGTON"}
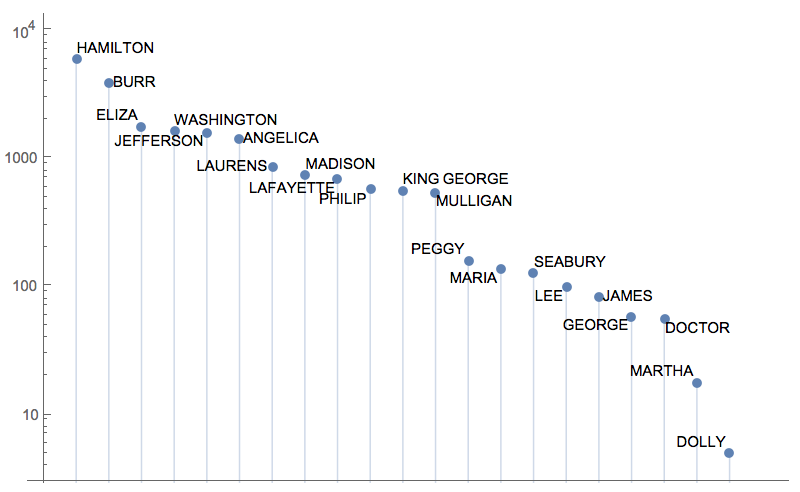
At this point it's easy to compute statistics on the lyrics. Here are the number of words each character sings, and a log plot:
Reverse[Sort[WordCount /@ Association[linesbycharacter]]]
ListLogPlot[%, Filling -> Axis, Ticks -> {None, Automatic}]
<|"HAMILTON" -> 5977, "BURR" -> 3889, "ELIZA" -> 1805, "WASHINGTON" -> 1634, "JEFFERSON" -> 1596, "ANGELICA" -> 1410,
"LAURENS" -> 854, "MADISON" -> 738, "LAFAYETTE" -> 688, "PHILIP" -> 572, "KING GEORGE" -> 568, "MULLIGAN" -> 543, "PEGGY" -> 162,
"MARIA" -> 137, "SEABURY" -> 128, "LEE" -> 99, "JAMES" -> 83, "GEORGE" -> 59, "DOCTOR" -> 56, "MARTHA" -> 18, "DOLLY" -> 5|>
And we can create word clouds for each character.
WordCloud["BURR" /. linesbycharacter, FontFamily -> "American Typewriter"]
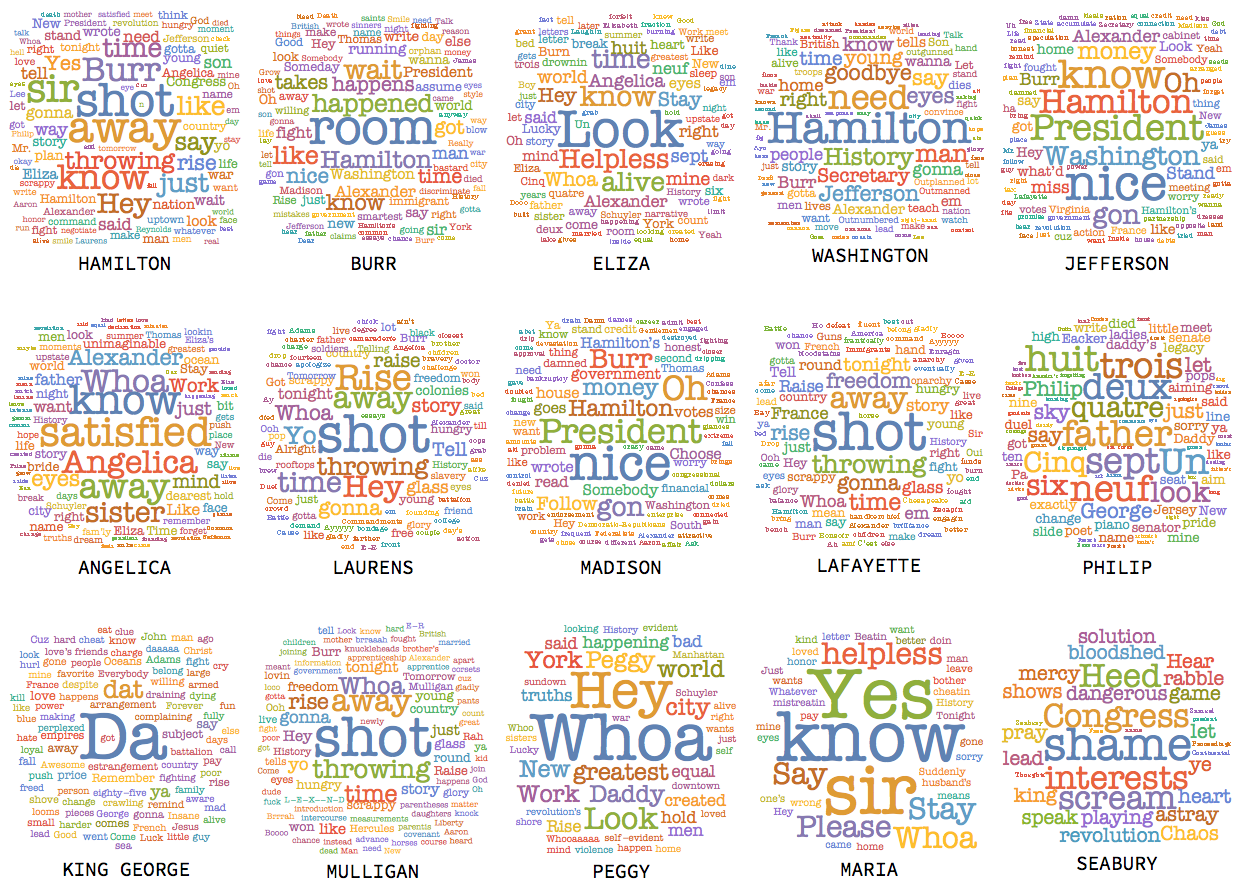
I posted a bunch of these on Twitter a while back.
Grid[Partition[
(Labeled[WordCloud[
StringReplace[TextWords[DeleteStopwords[
StringDelete[#1 /. linesbycharacter, "ev'ry" | "there'll", IgnoreCase -> True]]], "'" -> "\[CloseCurlyQuote]"],
FontFamily -> "American Typewriter"], #] &) /@
Keys[Take[Reverse[Sort[WordCount /@ Association[linesbycharacter]]], 15]],
5
]]
Okay, can we get back to politics? Let's construct the graph showing who mentions who. We have each character's lines, so now we have to extract mentions of each character from those lines. Again this isn't totally straightforward, because characters are referred to in multiple ways. Eliza never says "Hamilton" because she calls him "Alexander". Eliza refers to the Washington Monument but not Washington the person by name; but she does say "the General", so we'll count it. Here's what we get when we restrict to the 8 popular curve characters:
edges = Join @@ Thread /@ {
"Angelica" -> {"Angelica", "Burr", "Eliza", "Hamilton", "Jefferson"},
"Burr" -> {"Angelica", "Burr", "Eliza", "Hamilton", "Jefferson", "Washington"},
"Eliza" -> {"Angelica", "Eliza", "Hamilton", "Washington"},
"Hamilton" -> {"Angelica", "Burr", "Eliza", "Hamilton",
"Jefferson", "King George", "Lafayette", "Washington"},
"Jefferson" -> {"Burr", "Hamilton", "Lafayette", "Washington"},
"King George" -> {"Washington"},
"Lafayette" -> {"Burr", "Hamilton", "Lafayette"},
"Washington" -> {"Burr", "Hamilton", "Jefferson", "Lafayette"}
};
To draw the graph, let's pick some patriotic colors.
EntityValue[Entity["Country", "UnitedStates"], "Flag"]
{blue, red, white} = Union[Cases[%, _RGBColor, Infinity]]

Extract the blue from the Hamilton curve so we can replace it with the flag blue:
curveblue = First[Cases[EntityValue[Entity["PopularCurve", "HamiltonCurve"], "Image"], _RGBColor, Infinity]]

Here's the graph:
graph = Graph[edges,
EdgeShapeFunction -> GraphElementData[{"Arrow", "ArrowSize" -> .02, "ArrowPositions" -> .5}],
EdgeStyle -> red,
GraphLayout -> "LayeredDigraphEmbedding",
ImageSize -> 600,
PerformanceGoal -> "Quality",
VertexShapeFunction -> (Inset[Replace[EntityValue[Entity["PopularCurve", StringDelete[#2, Whitespace] <> "Curve"], "Image"] /.
curveblue -> blue, {(Axes -> _) -> Axes -> False, (ImageSize -> _) -> ImageSize -> 70}, {1}], #1] &)
]
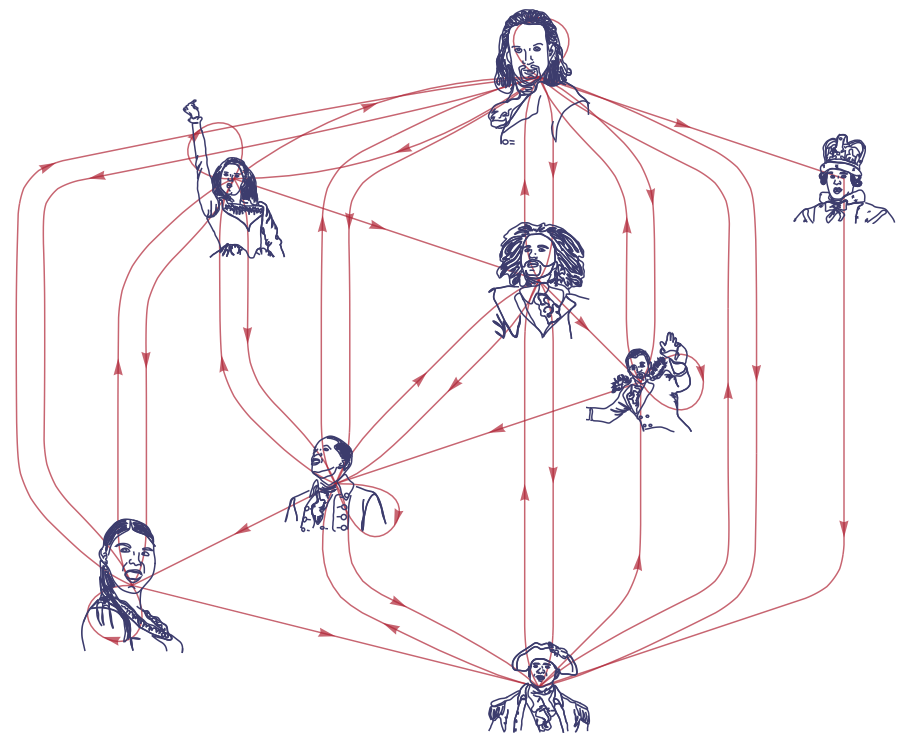
Is the graph Hamiltonian??? Wait for it...
HamiltonianGraphQ[graph]
True
Let's see a Hamiltonian cycle!
HighlightGraph[graph, First[FindHamiltonianCycle[graph]], GraphHighlightStyle -> "DehighlightGray"]
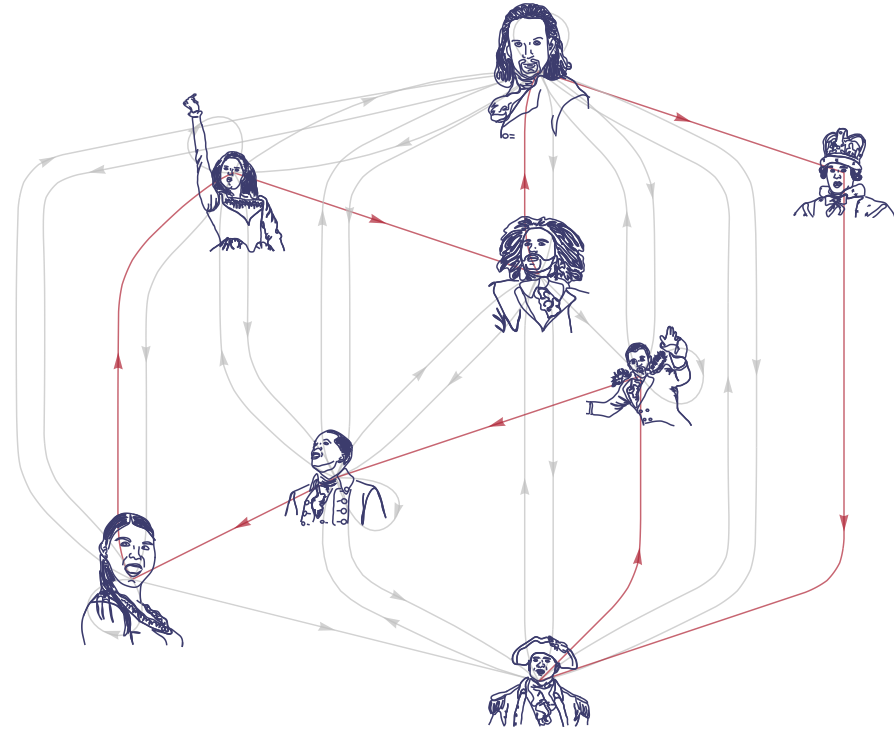
Just the cycle, without the other edges:
HighlightGraph[graph, First[FindHamiltonianCycle[graph]], GraphHighlightStyle -> "DehighlightHide"]
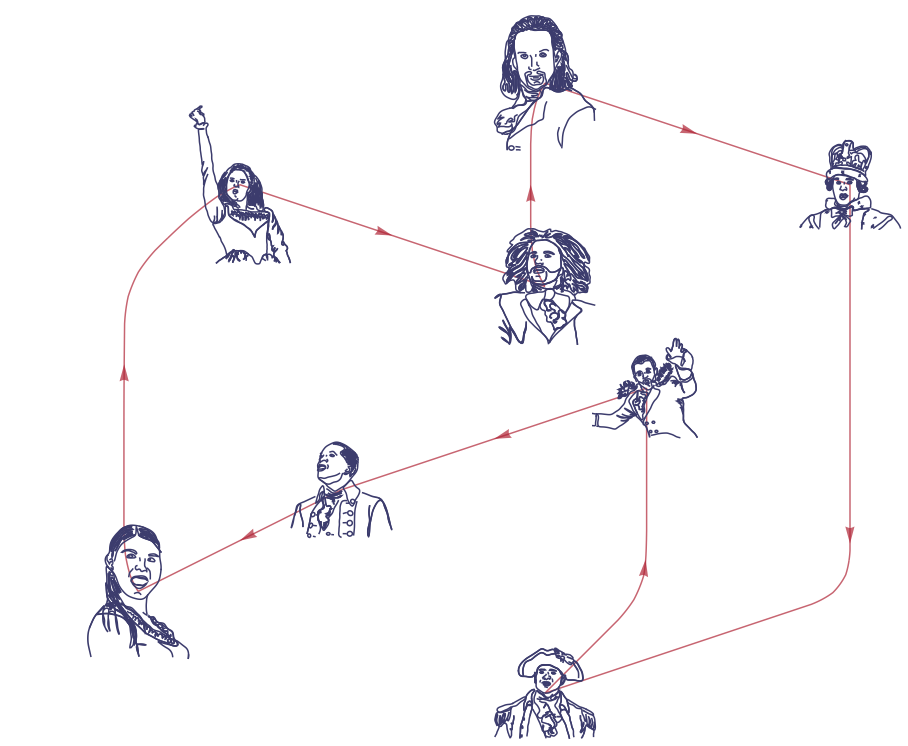
Here's a text version of the Hamiltonian cycle:
StringJoin[Riffle[(Append[#, First[#]] &)[RotateLeft[First /@ First[FindHamiltonianCycle[graph]], 2]], " mentions "]]
"Hamilton mentions King George mentions Washington mentions Lafayette mentions Burr mentions Eliza mentions Angelica mentions Jefferson mentions Hamilton"
So there we have it — a Hamiltonian Hamilton graph. For each edge in the graph, can you think of a line where character $A$ mentions character $B$?
And for bonus points.... can you now analyze the lyrics using quaternions?
 Attachments:
Attachments: