Given an irregular tetrahedron, with distinct non-collinear incenter, circumcenter, and centroid. Is there a unique triangle with the same incenter, circumcenter, and centroid? Seems so.
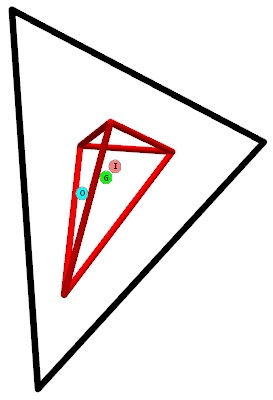
Here is code for that image.
ColoredLabeledPoint[color_RGBColor, text_String] := Graphics[{EdgeForm[{Gray}], color, Disk[{-.2, .1}, 1], Black,
Text[Style[text, Small], {0, 0}, FormatType -> StandardForm]}, ImageSize -> {15, 15}];
Graphics3D[{Text[ColoredLabeledPoint[Pink, "I"], {4, 5, 0}], Text[ColoredLabeledPoint[Cyan, "O"], {0, 0, 0}],
Text[ColoredLabeledPoint[Green, "G"], {3, 3, 0}], Black, Tube[#, .5] & /@ Subsets[
{{1/4 (49 + 31 Sqrt[3]), 1/4 (-31 + 49 Sqrt[3]), 0}, {1/4 (49 - 31 Sqrt[3]), 1/4 (-31 - 49 Sqrt[3]), 0}, {-(31/2), 49/2, 0}}, 2],
Red, Tube[#, .5] & /@ Subsets[{{0, -15, 0}, {0, 9, -12}, {12, 9, 0}, {0, 9, 12}}, 2]}, Boxed -> False]
Is there an easy way to find this triangle for a given tetrahedron? The same question on math.stackexchange. The method I used to find this example was very messy.