Reports from those who have mastered the mysterious doctrine of the escalator class, say that pentagonal symmetry gilds the penthouse of mathematics with recursions of divine proportion, that renaissance number theories drape walls with arithmetic splendor, that the highest Platonic solids find their natural pedestals, aloft from the greedy eyes and the dirty hands of mere mortals. Where the highrise rises--New York, Berlin, Paris, London, Rome, Boston, Kiev, Petersburg?--even that seems like a secret to the workaday mathematician, mining for a coal theorem, even for a lesser pastoral statement. Then there are daydreams, secret elevators that raise our thoughts to the treasures of Kings, Tsars, Kaisers, and other Lords, to filigreed topologies. Zzzzzz...
We start with an overlay of the icosahedron and dodecahedron adjacency graphs, with one graph point projected to infinity. On each graph we draw a Hamiltonian cycle, such that both cycles overlap in exactly two locations. This task is not exactly routine, requires a bit of hacking:
DodecaGraph = PolyhedronData["Dodecahedron", "SkeletonGraph"];
HackedVertices =
DeleteCases[
Chop[Mean[
PolyhedronData["Dodecahedron", "SkeletonCoordinates"][[
Union[Flatten[#]]]]] & /@ (FindCycle[DodecaGraph, 5, 12] /.
UndirectedEdge -> List)], {0, 0}];
ReHackedVertices =
ReplacePart[
HackedVertices, {1 -> 1.2 HackedVertices[[1]],
2 -> 1.2 HackedVertices[[2]], 10 -> 1.2 HackedVertices[[10]],
9 -> 1.2 HackedVertices[[9]], 11 -> 1.2 HackedVertices[[11]]}];
Show[DodecaGraph, Graphics[{Lighter@Red,
Line[ReHackedVertices[[#]]] & /@ {
{2, 3}, {3, 4}, {1, 3}, {2, 4}, {3, 5}, {5, 6}, {6, 4},
{5, 4}, {3, 7}, {7, 5}, {7, 1}, {6, 10}, {4, 10}, {5, 8},
{6, 8}, {7, 8}, {11, 6}, {11, 8}, {8, 9}, {7, 9}},
Arrow[{ReHackedVertices[[#]], 1.5 ReHackedVertices[[#]]}] & /@ {2,
1, 9, 11, 10},
{Opacity[0], EdgeForm[Directive[Lighter@Red]],
Disk[{0, 0}, Norm@ReHackedVertices[[1]]]},
{Opacity[0], EdgeForm[Directive[Thick, Darker@Red]],
Annulus[{0, 0}, {Norm@ReHackedVertices[[1]] - .001,
Norm@ReHackedVertices[[1]]}, {11 Pi/10, 15 Pi/10}]},
{EdgeForm[Thick], Lighter@Red,
Disk[#, .05] & /@ ReHackedVertices},
{Thick, Darker@Red,
Arrow[ReHackedVertices[[#]]] & /@ Partition[{2, 4, 3, 1}, 2, 1],
Arrow[ReHackedVertices[[#]]] & /@
Partition[{11, 8, 9, 7, 5, 6, 10}, 2, 1],
Arrow[{1.3 ReHackedVertices[[11]], ReHackedVertices[[11]]}],
Arrow[{ReHackedVertices[[1]], 1.5 ReHackedVertices[[1]]}],
Arrow[{ReHackedVertices[[2]] - {0.01, 0},
ReHackedVertices[[2]]}]}}],
Graphics[{
Darker@Darker@Blue, Thick,
FindHamiltonianCycle[DodecaGraph, 3][[1]] /.
UndirectedEdge[y_, z_] :> Arrow[{y, z}] /.
x_Integer :>
PolyhedronData["Dodecahedron", "SkeletonCoordinates"][[x]]}],
ImageSize -> 500
]
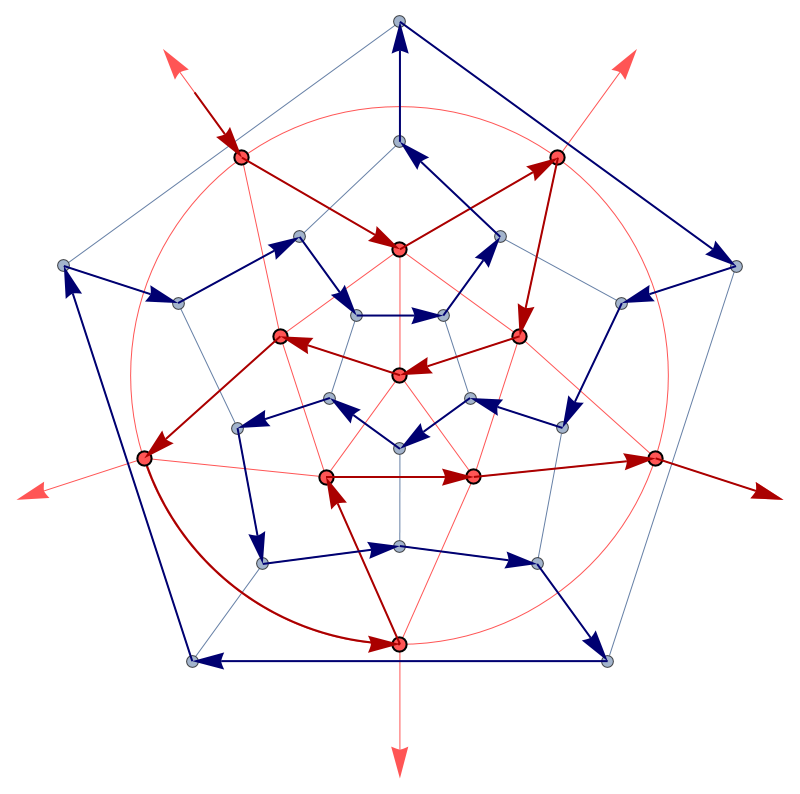
As required by the dual construction, edges on icosahedron / dodecahedron graph correlate 1-to-1. Now notice that every edge is at least covered by one link from either the icosahedral or the dodecahedral Hamiltonian cycle. On exactly two edges, the cycles overlap one another, and the edge is covered by a link from both Hamiltonian cycles. This topology of intersecting cycles gives meaning to the Euler Characteristic, $\chi$, from the famous VEF equation: $V-E+F=\chi=2$. Similar constructions are known to exist for the cube / octahedron pair and for the self-dual tetrahedron. Other similar constructions likely exists for irregular solids, but some polyhedra do not have Hamiltonian cycles, so the construction as-is does not apply in general.
The next part is difficult, relies on working knowledge of representation theory...
The Euler equation has an interesting analog in representation theory. For each platonic solid we know that $2E=|G|$, with $|G|$ the order of $G= A4 \; | \;S4\;|\; A5$ symmetry. For these groups, $V+E+F=|G|+2$. This leads naturally to a conjecture that a group representation simultaneously permuting labeled edges, faces, and vertices is almost regular : the irreducible decomposition is a superset of the regular representation's irreducible decomposition. It is known from basic theorems of representation theory that each permutation representation contains a copy of the one dimensional isotropic representation, call it $A$. The $V+E+F$ representation contains at least $3A$, when the regular contains only one $A$. In terms of representation theory, the Euler characteristic $\chi = 2$ counts the number of extra $A$ representations, relative to the regular representation. To determine this true, we need only reference the irreducible decompositions: $$E \longrightarrow A + T + 2G + 3H$$ $$V+F \longrightarrow 2A + 2T + 2G + 2H$$ $$V+F+E \longrightarrow 2A + ( A + 3T + 4G + 5H )$$ In the final decomposition, the part in parenthesis is just the irreducible decomposition of the regular representation, so the $E+V+F$ representation is almost regular per our definition above. It's also worthwhile to note that representations $V+F-2A$ and $E$ are not equivalent. Going back to the diagram above, there is obviously some deeper relation.
More can be done by formulating the permutation representations as matrices acting on a vector spaces. In this case it's easy to prove that the $V+F-2A$ representation is not equivalent to $E$ representation, simply by noting the transformation properties. The $E$ representation is a pure permutation representation, whereas the $V+F-2A$ is a signed permutation representation. Proof:
The vector elements transforming like isotropic A representations are summations over the unit vectors $v_{V,i},v_{F,i}$ corresponding to faces or vertices: $$v_ {A, F } = \sum_ {i}^{faces } v_ {F , i} $$ $$v_ {A, V } = \sum_ {i}^{vertices } v_ {V , i} $$ Every transformation leaves $v_{A,F}$, $v_{A,V}$ invariant. We can construct other vectors or "partners" that transform covariantly with a group representation, in particular V+F-2A. This is automated by the graph above if we write $$v_ {V + F - 2 A, i, j} = v_ {F, i} - v_ {F , j} $$ $$v_ {V + F - 2 A, i, j} = v_ {V, i} - v_ {V , j} $$ $$v_ {V + F - 2 A, i, j, k, l} = v_ {F, i} - v_ {F, j} + v_ {V, k} - v_ {V, l} $$ using the convention that the negative sign corresponds to the tail of an arrow while the positive sign corresponds to the head. We have $E-2$ vectors of the first two kinds and $2$ vectors of the third kind. It's easy to see that these vectors are orthogonal to the $A$ representation vectors. As well it is easy to see that the 30 vectors are linearly independent. The 30 vectors constitute a valid span for the vector space associated with representation V+F-2A. As with the edge permutation representation, all group operations in this representation map between links of the Hamiltonian cycle. The directedness of the Hamiltonian cycle carries over to the vector space, so when an arrow reverses direction under some rotation transformation, the permutation matrix will have a signed matrix element $-1$. This supports our assertion that "$V+F-2A$ is a signed permutation representation".
That is all for now, but if you are still interested, A. Ceulmans also has discovered some of this mathematics, and published a couple of articles regarding symmetry interpretations of the VEF equation: one, two. Zzzz... Not sure if any of this will make it into my dissertation, but it does seem worth the diversion.