Hi all, I'm writing cause i've a problem concerning the solution of the Fourier equation for thermodynamic in cylindrical coordinates: (1/r) d/dr (k r (dT/dr)) = ? c (dT/dt) r: radius t: time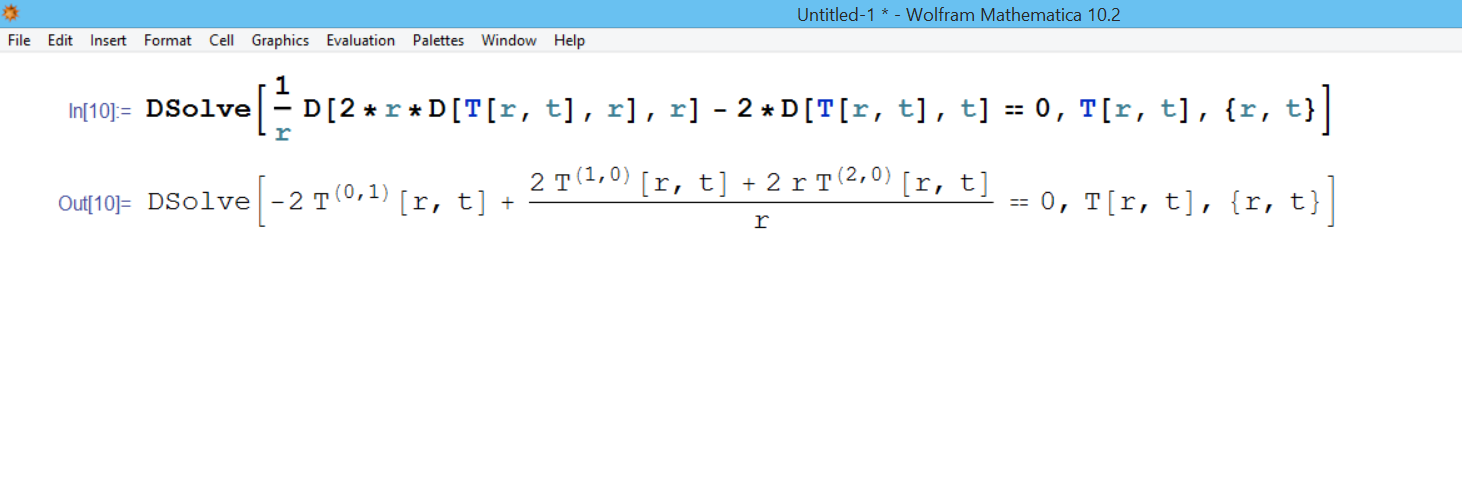 T: temperature ?,c,k: costants d= partial derivative I tried to solve it writing:

DSolve[1/r D[2*r*D[T[r, t], r], r] - 2*D[T[r, t], t] == 0, T[r, t], {r, t}]

where i put 2 instead of the constants. You can see the results in the image: It was the same than the input! Mathematica never gave me a result. I noticed that the problem is the second derivative, i tried to solve simpler differential equation with one derivative of 1st order, with 2 derivative of 1st order, with derivatives of 2nd order. The second derivative and the presence of 2 1st order derivative were always problems. Could you tell me where the error can be? Could you advise me about a possible "better way" to solve it? Thank you.