Hello, Let us consider the graph2:
z3 = {1 <-> 2, 2 <-> 3, 3 <-> 4, 4 <-> 5, 5 <-> 6, 6 <-> 7, 7 <-> 19,19 <-> 20, 19 <-> 22,
20 <-> 21, 20 <-> 23, 7 <-> 8, 8 <-> 24, 24 <-> 25, 24 <-> 26, 8 <-> 9, 9 <-> 10, 9 <-> 27,
27 <-> 28, 27 <-> 29, 10 <-> 11, 11 <-> 12, 12 <-> 13, 13 <-> 14, 14 <-> 15,15 <-> 16,
16 <-> 17, 17 <-> 18, 12 <-> 30, 30 <-> 31, 31 <-> 32, 32 <-> 33, 30 <-> 34, 31 <-> 35,
32 <-> 36, 34 <-> 37, 34 <-> 38, 2 <-> 39, 3 <-> 40, 4 <-> 41, 5 <-> 42, 6 <-> 43,
10 <-> 44, 11 <-> 45, 13 <-> 46, 14 <-> 47, 15 <-> 48, 16 <-> 49, 17 <-> 50,
18 <-> 51, 18 <-> 52, 1 <-> 53, 1 <-> 54};
graph2= Graph[z3,GraphLayout -> "SpringEmbedding",(*VertexLabels\[Rule]"Name",*)EdgeStyle -> Thick]
The color version looks like this:
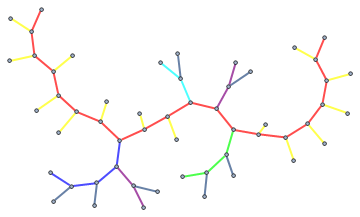
The question is: How can we get graph2 from the graph1?
z1 = {1 <-> 2, 1 <-> 3, 1 <-> 4, 1 <-> 5, 1 <-> 6, 1 <-> 7, 1 <-> 8,1 <-> 9, 1 <-> 10, 1 <-> 11,
1 <-> 12, 9 <-> 13, 1 <-> 14, 1 <-> 15,1 <-> 16, 12 <-> 17, 1 <-> 18, 12 <-> 19, 12 <-> 20,
1 <-> 21,1 <-> 22, 1 <-> 23, 8 <-> 24, 4 <-> 25, 4 <-> 26, 20 <-> 27};
graph1 = Graph[z1, GraphLayout -> "RadialDrawing"(*,VertexLabels\[Rule]"Name"*)]
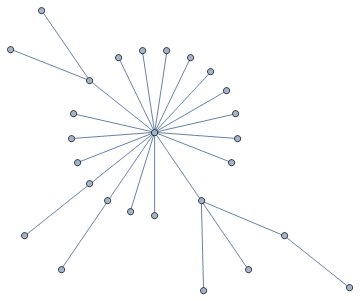
Let us imagine that it is a network of streets. Red trail markes the longest street. The longest street connects directly to 18 smaller streets - this is the degree of the middle vertex in graph1. The second longest street is dark blue - this street connects to three other streets... and so on... In this way we obtain the graph1. I wrote a script which calculates graph1 based on graph2 (for very large networks). Another hint: If the graph2 will have the structure like this:
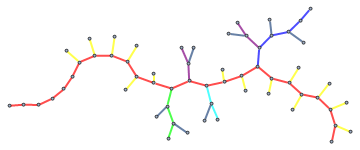
then the graph1 will be the same. However, if we start from the graph1 we should obtain graph2 (the first graph from the top i.e. z3).