Hi, in my current project i evaluate large sums of the form:
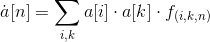
in the most cases f(i,k,n)=0 so im left with expressions of the form
b*a[3]*a[4] + c*a[4]*a[3] + ...
what i want are expresions of the form like:
(b+c)*a[3]* a[4]
Sometimes Simplify or FullSimplify is doing the job sometimes not...
An example of what such an result look like is attached.
Not my plan was to go through the expression and find all components which are proportional to a[i]*a[k] and sum up the prefactors, but i cant figure out a nice way of doing that.
Does someone have an idea how to put the expression in the right form?
Many thanks in advance!!!
 Attachments:
Attachments: