This was originally in reply to somebody else, but it appears that just before I posted the original thread was removed. I thought I might as well post anyway though. The question was asking about something to find the shortest route to walk a dog to a pet store, coffee shop, park, etc from some starting location.
Here is something that does this with the Yelp ServiceConnector, so you will need to make a Yelp account for this to work.
First we can define a function that finds the nearest few places in a certain category.
findCategories[loc_, categories_, maxCount_: 1] :=
ServiceExecute["Yelp", "BusinessList", {"Location" -> loc, "Categories" -> categories, MaxItems -> maxCount, "SortBy" -> "Distance"}][[All, {"Name", "Coordinate"}]]
This will return a list of places that fall into a certain category near the specified location. Each of these places is represented with its name and its location. The categories come from Yelp's category list.
We can find the nearest few places in each of these categories because the nearest one to the starting location is not necessarily the one that gives you the shortest total route. We can then make a function that will find the shortest tour with a few of these places.
planWalk[loc_, stops_] :=
Last@Keys@Sort@Flatten@Outer[
(tour \[Function] {##}[[tour[[2]]]] -> tour[[1]])@FindShortestTour[{##}[[All, "Coordinate"]]] &,
Sequence @@ Prepend[findCategories[loc, #, 5] & /@ stops, {<|"Name" -> "Home", "Coordinate" -> loc|>}]
]
Basically, this finds the nearest 5 places in each category and then finds the set with one from each category that has the shortest tour. This is finding the shortest tour by GeoDistance though. You might want it by TravelDistance, but TravelDistance is much much slower than GeoDistance. (The DistanceFunction option for FindShortestTour also has to be symmetric, which TravelDistance isn't generally, but it seems to be when TravelMethod -> "Walking".)
Here is another version of the same function, but instead of using GeoDistance it uses TravelDistance, and it only finds the shortest tour for the nearest places, instead of considering the 5 nearest places from each category.
planWalk[loc_, stops_] :=
With[{places = Prepend[findCategories[loc, #, 1][[1]] & /@ stops, <|"Name" -> "Home", "Coordinate" -> loc|>]},
places[[FindShortestTour[places[[All, "Coordinate"]], DistanceFunction -> (QuantityMagnitude[TravelDistance[{##}, TravelMethod -> "Walking"], "Meters"] &)][[2]]]]
]
For the one example I tried, the second implementation took much longer to run (still less than a minute, but the first implementation was just a second or so), and gave a very similar result.
This function is a bit general, but for your specific case we might try something like this.
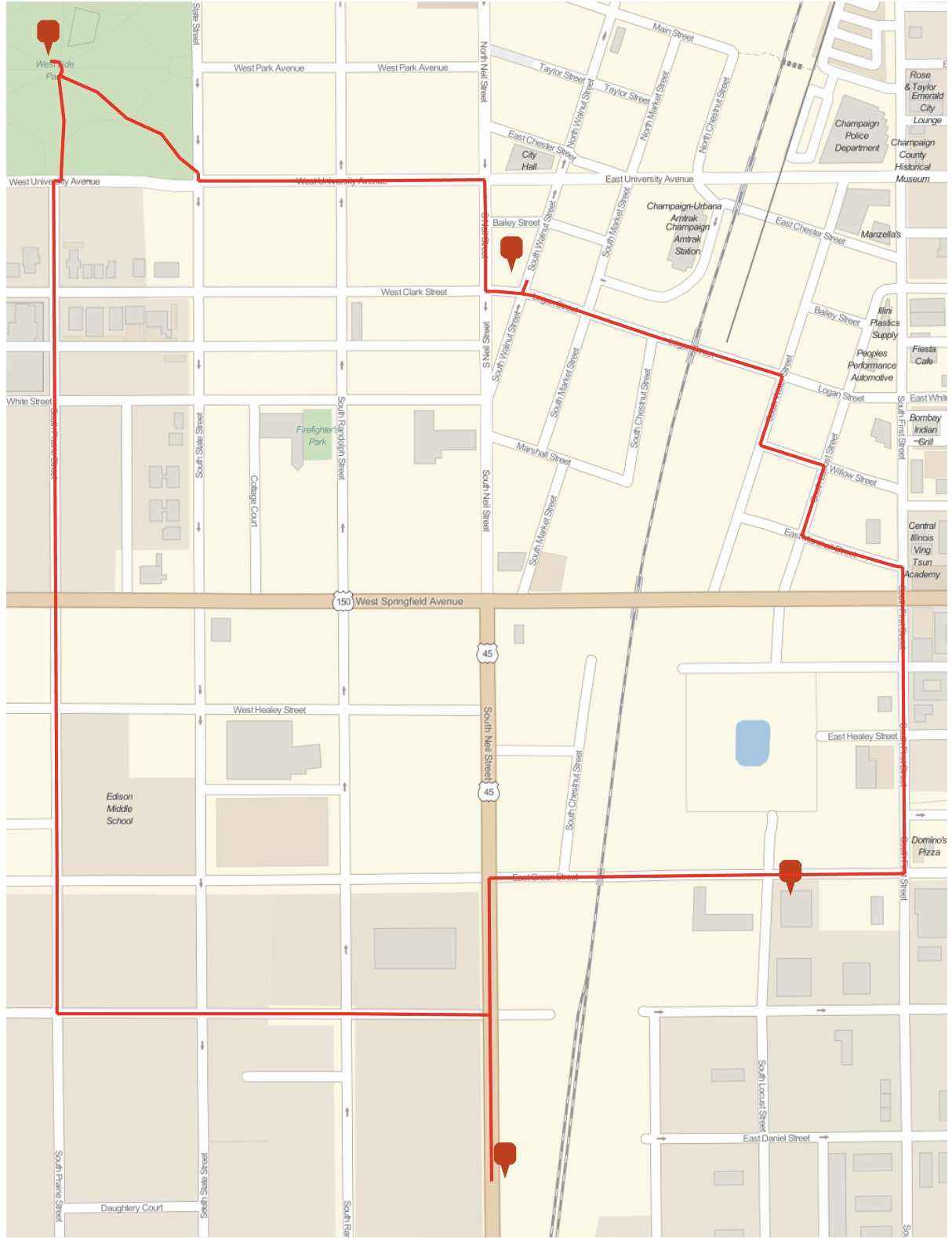
In[]:= plan = planWalk[GeoPosition[{40.11`, -88.24`}], {{"parks", "dog_parks"}, "petstore","coffee"}]
Out[]= {
<|Name->Home,Coordinate->GeoPosition[{40.11,-88.24}]|>,
<|Name->Walnut Street Tea,Coordinate->GeoPosition[{40.1155,-88.2432}]|>,
<|Name->West Side Park,Coordinate->GeoPosition[{40.1174,-88.2485}]|>,
<|Name->Sailfin Pet Shop,Coordinate->GeoPosition[{40.1075,-88.2433}]|>,
<|Name->Home,Coordinate->GeoPosition[{40.11,-88.24}]|>}
We can then calculate some more information about this plan.
In[]:= TravelDistance[plan[[All, "Coordinate"]], TravelMethod -> "Walking"]
Out[]= Quantity[2.33843, "Miles"]
In[]:= TravelTime[plan[[All, "Coordinate"]], TravelMethod -> "Walking"]
Out[]= Quantity[45, "Minutes"]
GeoGraphics[{Tooltip[GeoMarker[#Coordinate], #Name] & /@ plan, Red, Thick, GeoPath@TravelDirections[plan[[All, "Coordinate"]], TravelMethod -> "Walking"]}, ImageSize -> 600]
(On a side note, it probably wouldn't be hard to make a nice FormFunction out of this...)
 Attachments:
Attachments: