This is more difficult to explain:

myDerivationRule = 
  Derivative[i__ /; Total[{i}] == 1][f][x__] :> 
   f[x] Derivative[i][F][x];
D[f[x1, x2], x2] == (D[f[x1, x2], x2] /. myDerivationRule)
D[%, x1] /. myDerivationRule
D[%, x1] /. myDerivationRule

Hi Celement,

I think the best way is to use Faa Di Bruno's formula, which gives a nice generalization of the chain rule. Compare the following one-line calc. codes:

DerivativeList1[n_] :=  With[{rep = Rule[D[f[x], {x, #}] /. x -> F[x], 1] & /@ Range[n]},
  (D[f[F[x]], {x, #}] & /@ Range[n]) /. rep]
DerivativeList2[n_] :=  Table[BellY[i, j, D[F[x], {x, #}] & /@ Range[n]], {i, 1, n}, {j, 1, i}]    

Short of doing the recursive analysis, you can see that these are ouput equivalent by writing a logical function that applies SameQ to the output and returns true for any $n$. You should also check the timing statistics:

t1 = AbsoluteTiming[DerivativeList1[#];][[1]] & /@ Range[30]
t2 = AbsoluteTiming[DerivativeList2[#];][[1]] & /@ Range[30]

which show that BellY does much better than the naive implementation. However, in other threads I have shown that the current implementation of BellY is slow, and that's true again here. Using the recursion relations we get more time savings

DerivativeList3[n_] := Table[B2[i, j], {i, 1, n}, {j, 1, i}]
t3 = AbsoluteTiming[
     Clear@B2;
     B2[0, 0] = 1;
     B2[n_ /; n > 0, 0] := 0;
     B2[0, k_ /; k > 0] := 0;
     B2[n_ /; n > 0, k_ /; k > 0] := 
      B2[n, k] =        Total[Binomial[n - 1, # - 1] D[F[x], {x, #}] B2[n - #, 
            k - 1] & /@ Range[1, n - k + 1]];
     DerivativeList3[#];][[1]] & /@ Range[30]
ListLinePlot[{t1, t2, t3}, PlotStyle -> {Red, Orange, Green}]

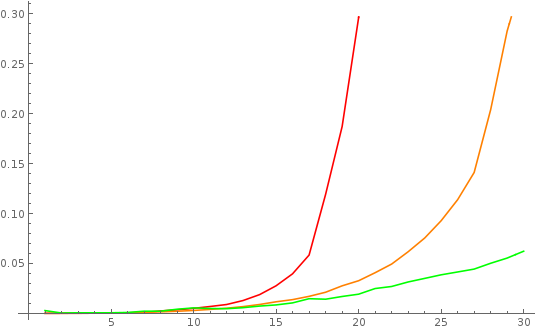
and the output up to $n=5$ :

DerivativeList1[5] // TableForm
DerivativeList2[5] // TableForm
DerivativeList3[5] // TableForm

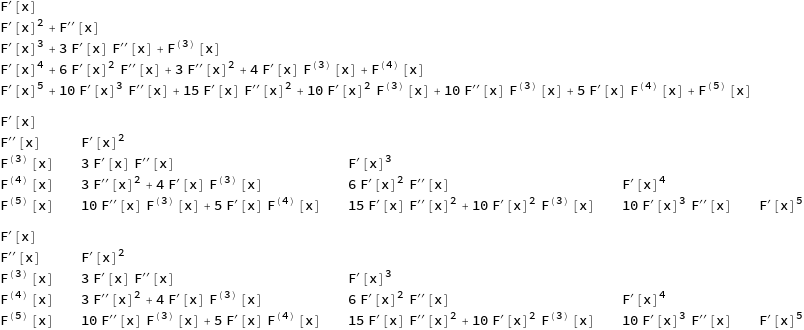
Brad

Edit: Code from Gianluca Gorni seems to be time-equivalent to the naive implementation above:

myDerivationRule = f'[x_] :> f[x]*F'[x];
AbsoluteTiming[  NestList[D[#, x] /. myDerivationRule &, f[x]*F'[x], 30] /. f[x] -> 1;][[1]]
Out[]=3.14197(s)

Oh, wow! An unexpected approximation of Pi.

To reduce confusion, consider a simplified version:

myDerivationRule = f'[x] -> f[x]*F'[x];
D[f[x]*F'[x], x] /. myDerivationRule

The arrow -> stands for a replacement rule: it instructs to replace f'[x] with f[x]*F'[x]. We store this replacement rule in the symbol myDerivationRule, so that it is easier to apply repeatedly.

Then consider f[x]*F'[x] and take its derivative with respect to x, i.e., D[f[x]*F'[x], x]. We get

f'[x] F'[x] + f[x] F''[x]

We want to replace f'[x] in this expression with f[x]*F'[x]. This is done with our replacement rule, which is applied with the shorthand slash-dot /.

D[f[x]*F'[x], x] /. myDerivationRule

After the replacement is done, we get the desired formula f[x]F'[x]^2+f[x]F''[x].

You can try something like this:

myDerivationRule = f'[x_] :> f[x]*F'[x];
f'[x] == f[x]*F'[x]
D[%, x] /. myDerivationRule
D[%, x] /. myDerivationRule
D[%, x] /. myDerivationRule