Message Boards Message Boards

Doodling in Mathematica: DRAGON TREES

Last week Vi Hart submitted a new class titled “Doodling in Math Class: DRAGONS”. There, she introduced a family of fractals known as dragon curves, see here below the most famous one, the Heighway dragon:
The Heighway dragon (also known as the Harter–Heighway dragon or the Jurassic Park dragon) was first investigated by NASA physicists John Heighway, Bruce Banks, and William Harter. It was described by Martin Gardner in his Scientific American column Mathematical Games in 1967. Many of its properties were first published by Chandler Davis and Donald Knuth. It appeared on the section title pages of the Michael Crichton novel Jurassic Park.
? Wikipedia


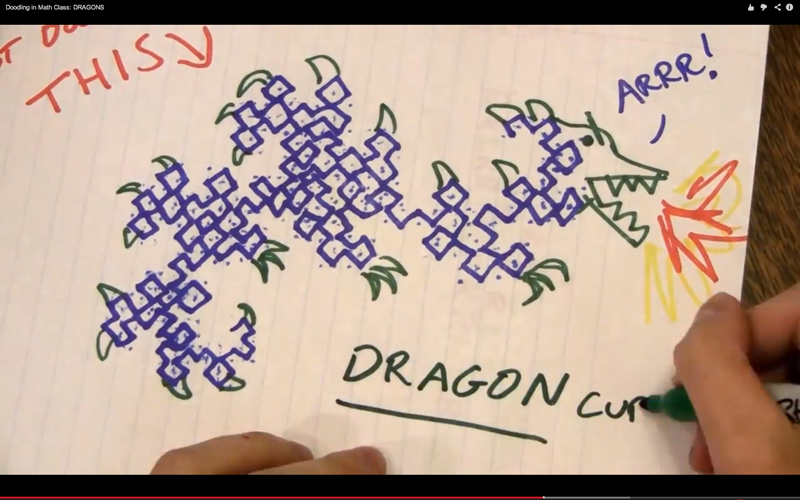
Wouldn’t it be great to doodle fractals as fast as she does? What about doodling dragons in Mathematica?



Two years ago, when I was playing with the mind-blowing “Tree Bender” demonstration by Theodore Gray, I spotted a striking property. When the two branch-locators were placed in a symmetrical arrangement along the pair of horizontal line-segments {{-0.5,0.5},{0.5,0.5}} and {{-0.5,-0.5},{0.5,-0.5}}, the resulting trees were always forming dragons! 



I was so excited by this observation that I ended up carrying out a whole project about fractal trees, I published two papers presenting the n-ary symmetric trees with tip-to-tip self-contact, I 3D-printed some SuperFractals generated by these trees, and I generalized this special class of fractals to three dimensional fractal trees during my participation at the 2013 Wolfram Science Summer School. For now let’s focus on doodling dragons, I will talk about these related projects in future discussions.

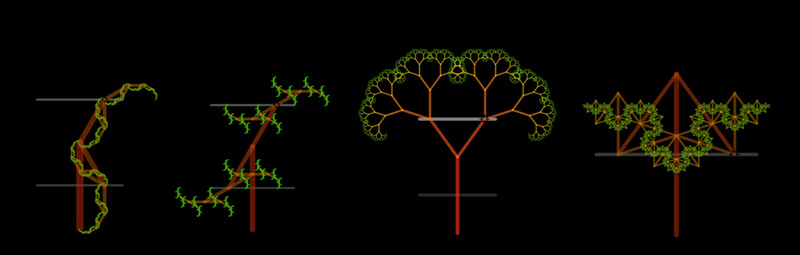
There are four different ways to place symmetrically the pair of locators along the pair of horizontal lines:
  1. One with the first pair of branches constrained to move along the upper line in a mirror symmetric way: Lévy Trees.
  2. One with the first pair of branches constrained to move along the lower line in a mirror symmetric way: Koch Trees.
  3. One with the first pair of branches constrained to move along both horizontal lines in an opposite way to each other, 180º: Polynomial Trees.
  4. And one with the first pair of branches constrained to move along both horizontal lines in a mirror symmetric way: Jurassic Park Trees.








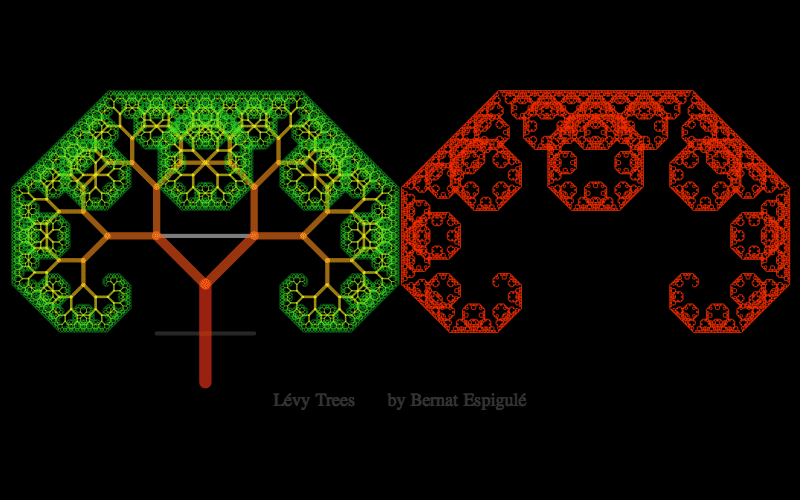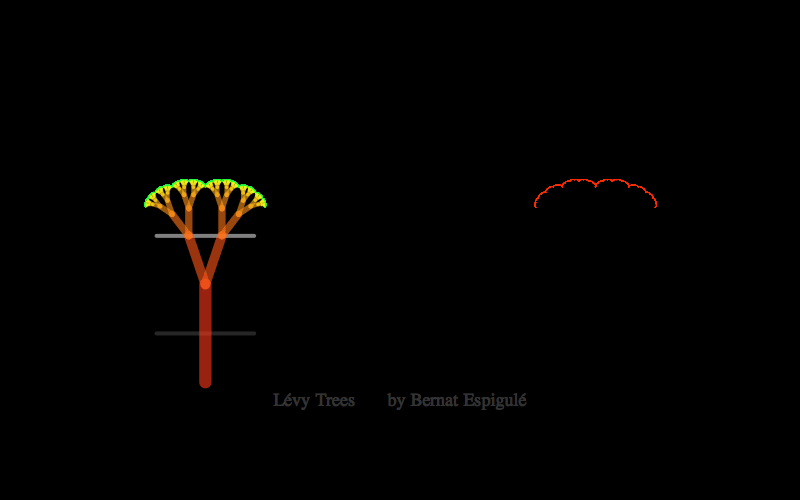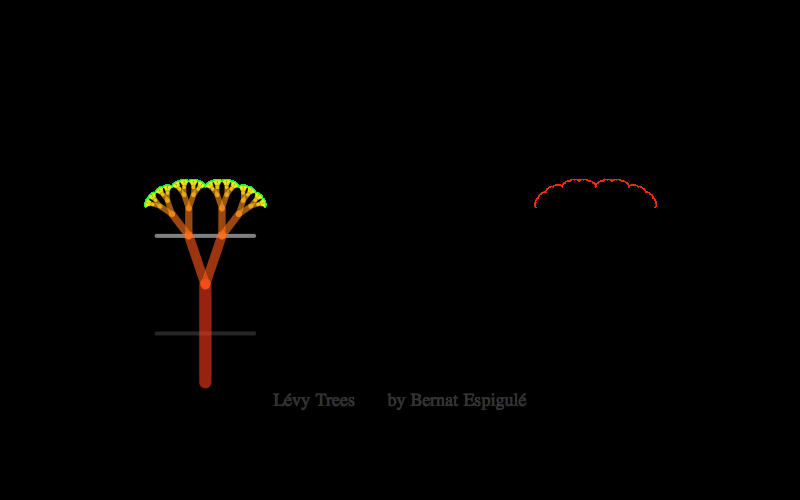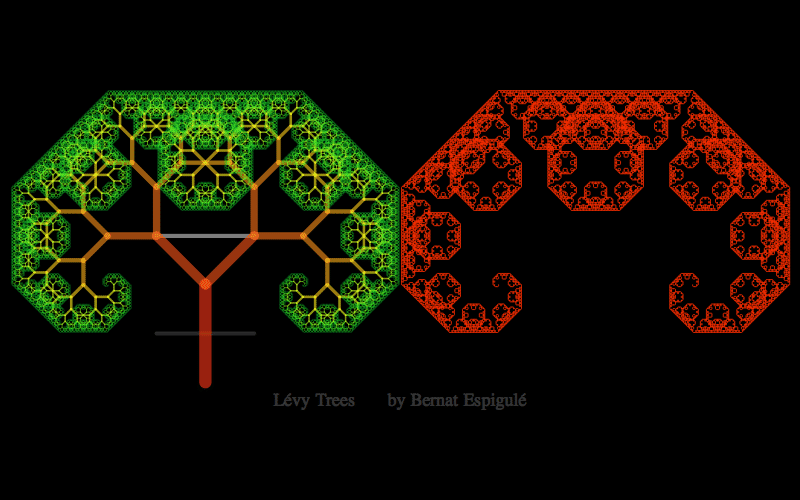
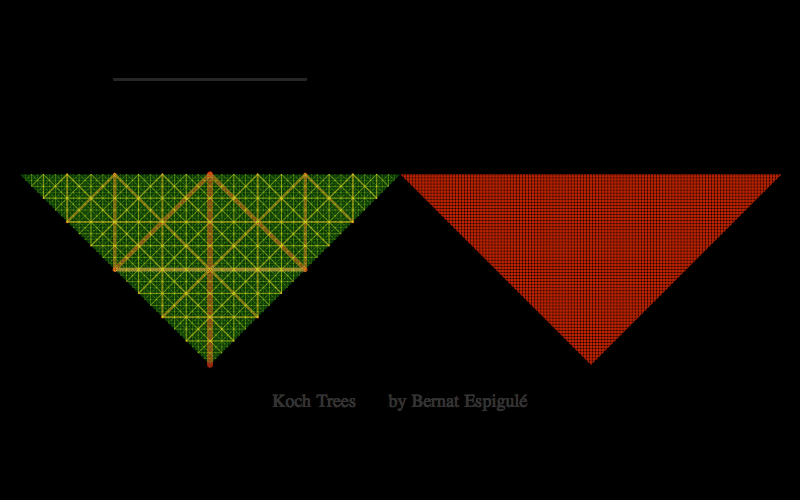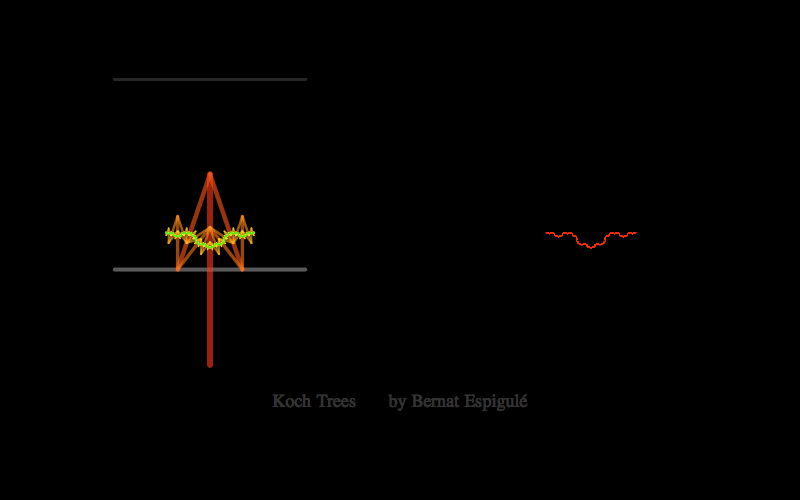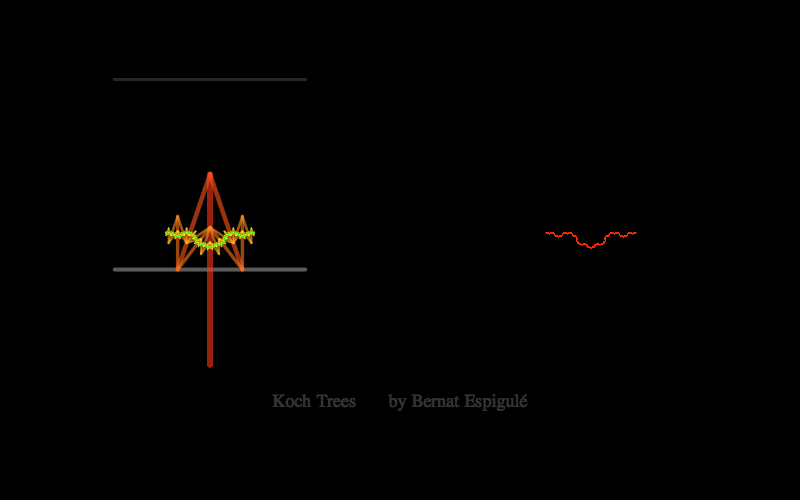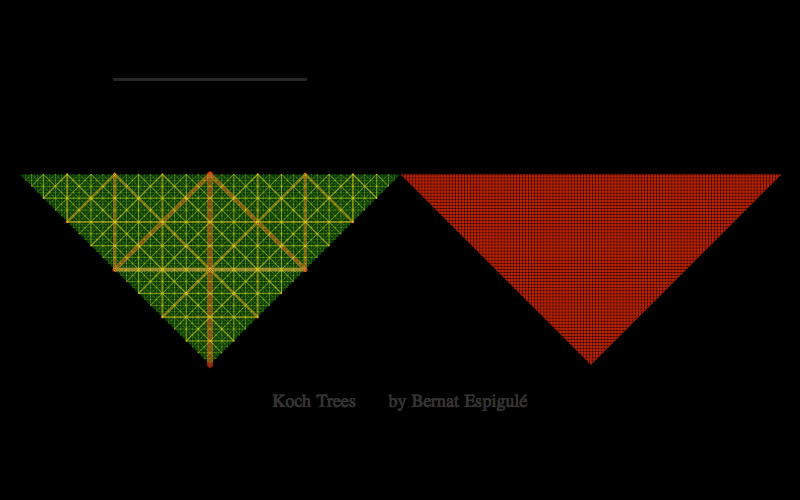
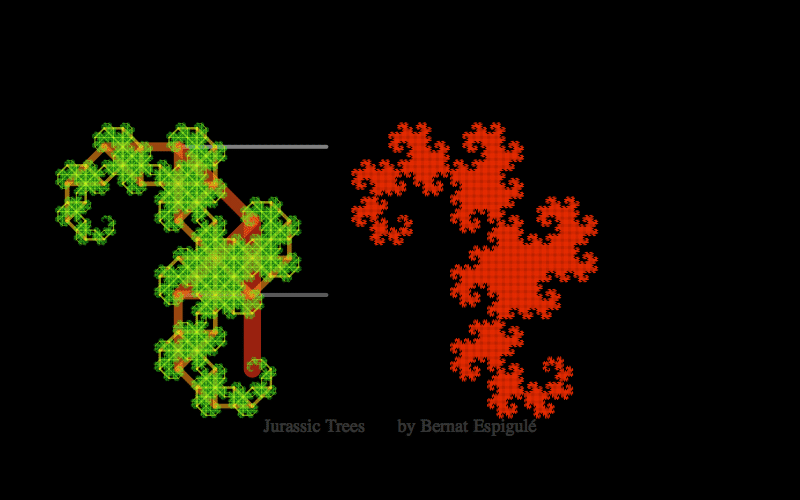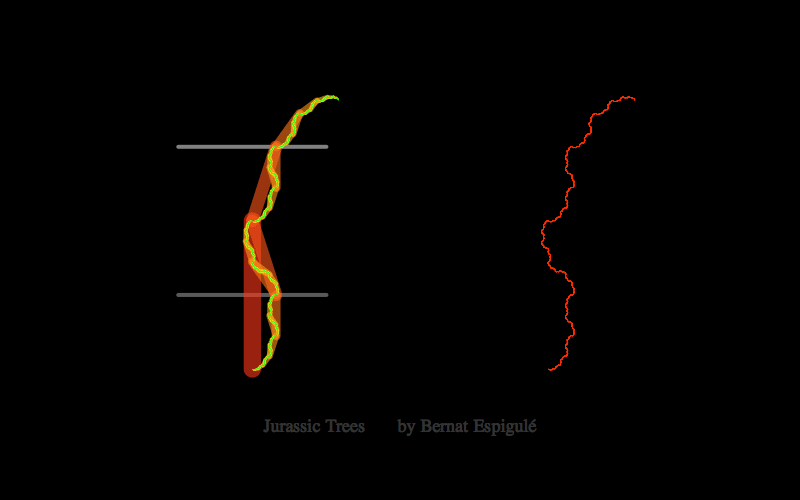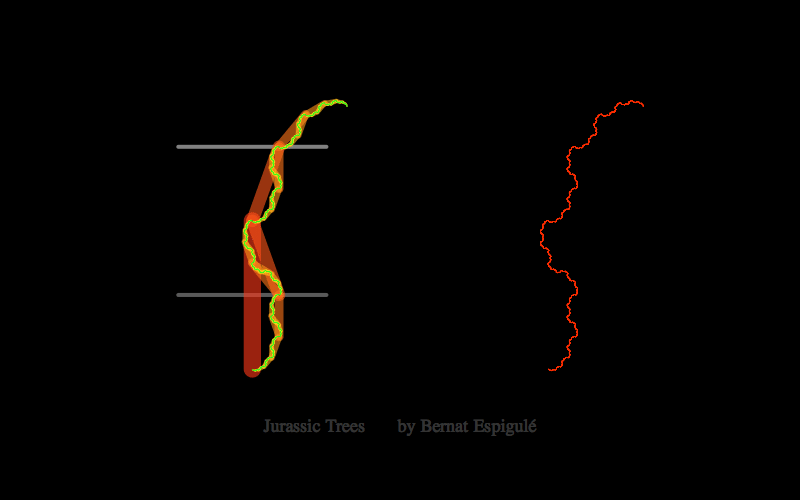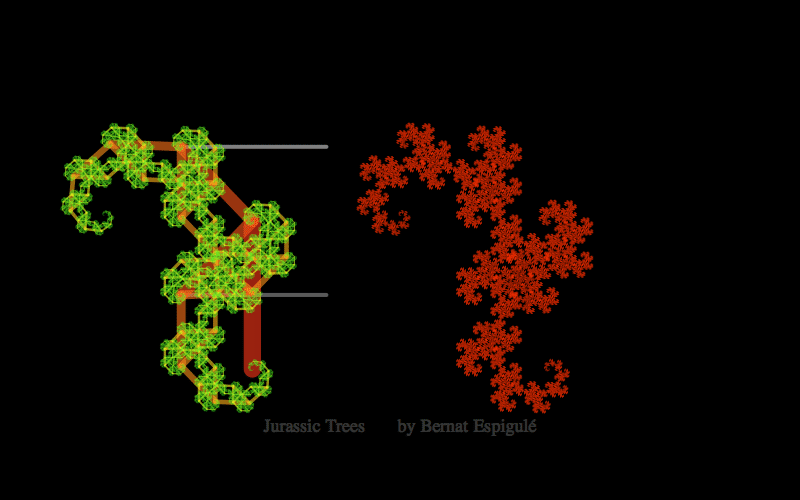
Here below you have my pieces of code for doodling the four different kinds of binary dragon trees. Notice that I’ve also added the final leaves in red and some meaningful labels to explore these trees with high precision (press Alt-key while moving the branch locator to slowly change the parameters).


Lévy Trees Doodler


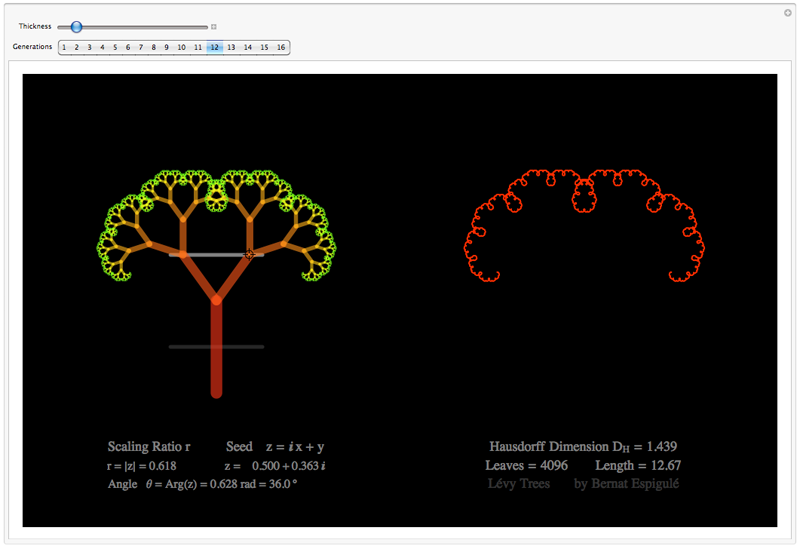
 Manipulate[
 Module[{branches=NestList[Flatten[Map[{{#[[2]],#[[2]]+{Reverse[{pt1[[1]],0.5}],{-1,1}*{pt1[[1]],0.5}}.(#[[2]]-#[[1]])},{#[[2]],#[[2]]+{Reverse[{-pt1[[1]],0.5}],{-1,1}*{-pt1[[1]],0.5}}.(#[[2]]-#[[1]])}}&,#],1]&,{{{0,-1},{0,0}}},gen]},
 Graphics[{
 {CapForm["Round"],Gray,Thickness[0.005],Opacity[0.3],Line[{{-0.5,-0.5},{0.5,-0.5}}]},
 {CapForm["Round"],Gray,Thickness[0.005],Line[{{-0.5,0.5},{0.5,0.5}}]},
 {(*Tree*)MapIndexed[{Hue[0.022*#2[[1]],0.9,1,0.6],CapForm["Round"],Thickness[th*0.77^#2[[1]]],Line[#]}&,branches]},
 {(*Leaves*)MapIndexed[{Hue[0.03(*gen*),1,1,0.9],CapForm["Round"],Thickness[th*0.82^(gen+1)],Translate[Line[#],{4,0}]}&,Drop[branches,gen]]},
 (*Labels*)
 {Inset[Style[Text@TraditionalForm@Style[Row[{"Scaling Ratio r"," ""       "" Seed    z = ",y+x*I}],18],Gray],{0,-1.6}]},
{Inset[Style[Text@TraditionalForm@Style[Row[{"r = |z|"," = ",SetAccuracy[Norm[{{pt1[[1]],0.5},{0,0}}],4],"                ",z," =    ",SetAccuracy[0.5,4]+SetAccuracy[pt1[[1]],4]I}],16],Gray],{0,-1.8}]},
{Inset[Style[Text@TraditionalForm@Style[Row[{"Angle   \[Theta] = Arg(z)"," = ",SetAccuracy[VectorAngle[{pt1[[1]],0.5},{0,0.5}],4]," rad = ",SetAccuracy[180/Pi*VectorAngle[{pt1[[1]],0.5},{0,0.5}],2]"\[Degree]         "}],16],Gray],{0,-2}]},
{Inset[Style[Text@TraditionalForm@Style[Row[{"Hausdorff Dimension \!\(\*SubscriptBox[\(D\), \(H\)]\) = ",SetAccuracy[ Log[2]/Log[1/Norm[{{pt1[[1]],0.5},{0,0}}]],4]}],18],Gray],{4.,-1.6}]},
{Inset[Style[Text@TraditionalForm@Style[Row[{"Leaves = ",Count[Drop[branches,gen],_Real,\[Infinity]]/4" ""     ""Length = ",SetAccuracy[Count[Drop[branches,gen],_Real,\[Infinity]]/4*(Norm[{{pt1[[1]],0.5},{0,0}}]^gen),3]}],18],Gray],{4.,-1.8}]},
{Inset[Style[Text@TraditionalForm@Style[Row[{"Lévy Trees       by Bernat Espigulé"}],18],Gray, Opacity[0.4]],{4.,-2}]}},
PlotRange->{{-2.1,6.1},{-2.1,2.1}},ImageSize->{1000,600},Background->Black]],
{{th,0.02,"Thickness"},0.005,0.185},
{{gen,12,"Generations"},Range[1,16], ControlType -> SetterBar},
{{pt1,{0.5,0.5}},{-0.5,0.5},{0.5,0.5},Locator}]

Koch Trees Doodler


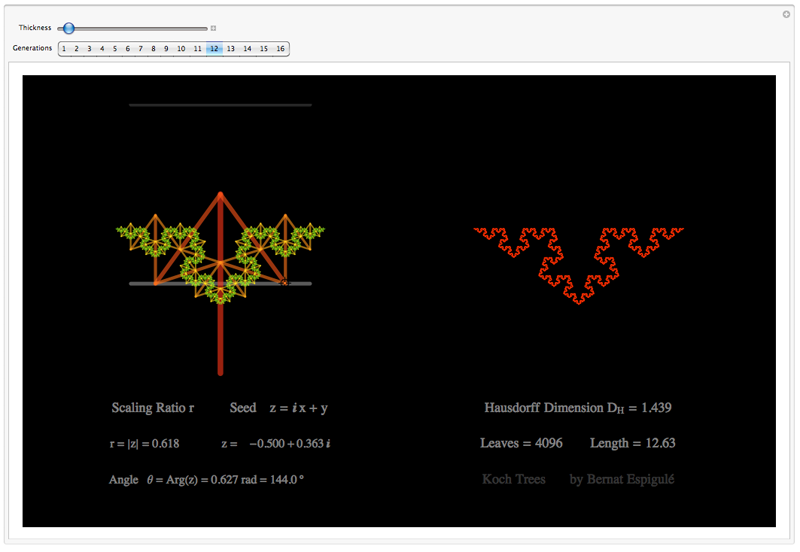
 Manipulate[
 Module[{branches=NestList[Flatten[Map[{{#[[2]],#[[2]]+{Reverse[{pt1[[1]],-0.5}],{-1,1}*{pt1[[1]],-0.5}}.(#[[2]]-#[[1]])},{#[[2]],#[[2]]+{Reverse[{-pt1[[1]],-0.5}],{-1,1}*{-pt1[[1]],-0.5}}.(#[[2]]-#[[1]])}}&,#],1]&,{{{0,-1},{0,0}}},gen]},
 Graphics[{{CapForm["Round"],Gray,Thickness[0.005],Opacity[0.7],Line[{{-0.5,-0.5},{0.5,-0.5}}]},{CapForm["Round"],Gray,Opacity[0.3],Thickness[0.005],Line[{{-0.5,0.5},{0.5,0.5}}]},
 {(*FrTree*)MapIndexed[{Hue[0.022*#2[[1]],0.9,1,0.6],CapForm["Round"],Thickness[th*0.75^#2[[1]]],Line[#]}&,branches]},
 {(*Red Leaves*)MapIndexed[{Hue[0.03(*gen*),1,1,0.9],CapForm["Round"],Thickness[th*0.84^(gen+1)],Translate[Line[#],{2,0}]}&,Drop[branches,gen]]},
 (*Labels*)
 {Inset[Style[Text@TraditionalForm@Style[Row[{"Scaling Ratio r"," ""       "" Seed    z = ",y+x*I}],18],Gray],{0,-1.2}]},
 {Inset[Style[Text@TraditionalForm@Style[Row[{"r = |z|"," = ",SetAccuracy[Norm[{{pt1[[1]],0.5},{0,0}}],4],"              ",z," =    ",SetAccuracy[-0.5,4]+SetAccuracy[pt1[[1]],4]I}],16],Gray],{0,-1.4}]},
 {Inset[Style[Text@TraditionalForm@Style[Row[{"Angle   \[Theta] = Arg(z)"," = ",SetAccuracy[VectorAngle[{pt1[[1]],0.5},{0,0.5}],4]," rad = ",SetAccuracy[180/Pi*VectorAngle[{pt1[[1]],-0.5},{0,0.5}],2]"\[Degree]         "}],16],Gray],{0,-1.6}]},
{Inset[Style[Text@TraditionalForm@Style[Row[{"Hausdorff Dimension \!\(\*SubscriptBox[\(D\), \(H\)]\) = ",SetAccuracy[ Log[2]/Log[1/Norm[{{pt1[[1]],0.5},{0,0}}]],4]}],18],Gray],{2.,-1.2}]},
{Inset[Style[Text@TraditionalForm@Style[Row[{"Leaves = ",Count[Drop[branches,gen],_Real,\[Infinity]]/4" ""     ""Length = ",SetAccuracy[Count[Drop[branches,gen],_Real,\[Infinity]]/4*(Norm[{{pt1[[1]],0.5},{0,0}}]^gen),3]}],18],Gray],{2.,-1.4}]},
{Inset[Style[Text@TraditionalForm@Style[Row[{"Koch Trees       by Bernat Espigulé"}],18],Gray, Opacity[0.4]],{2.,-1.6}]}},
PlotRange->{{-1.1,3.1},{-1.7,0.5}},ImageSize->{1000,600},Background->Black]],
{{th,0.01,"Thickness"},0.005,0.185},
{{gen,12,"Generations"},Range[1,16], ControlType -> SetterBar},
{{pt1,{0.5,0.5}},{-0.5,-0.5},{0.5,-0.5},Locator}]

Polynomial Trees Doodler


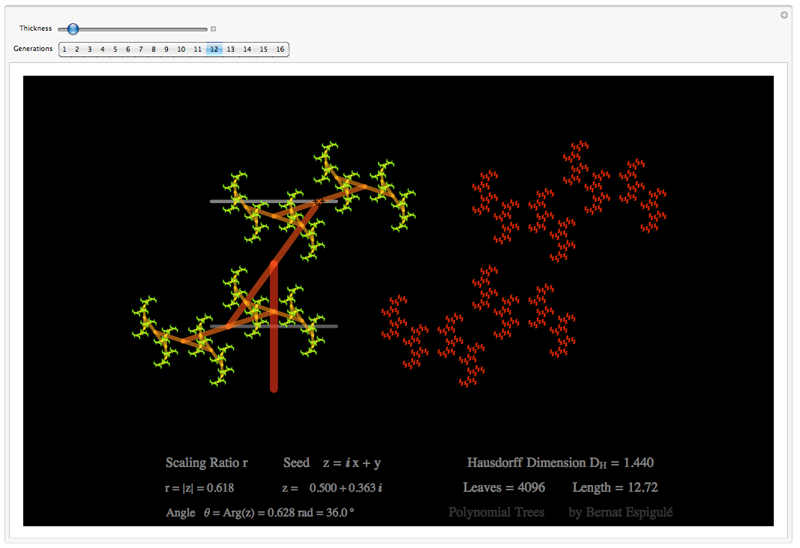
 Manipulate[
 Module[{branches=NestList[Flatten[Map[{{#[[2]],#[[2]]+{Reverse[{pt1[[1]],0.5}],{-1,1}*{pt1[[1]],0.5}}.(#[[2]]-#[[1]])},{#[[2]],#[[2]]+{Reverse[{-pt1[[1]],-0.5}],{-1,1}*{-pt1[[1]],-0.5}}.(#[[2]]-#[[1]])}}&,#],1]&,{{{0,-1},{0,0}}},gen]},
 Graphics[{{CapForm["Round"],Gray,Thickness[0.005],Opacity[0.7],Line[{{-0.5,-0.5},{0.5,-0.5}}]},{CapForm["Round"],Gray,Thickness[0.005],Line[{{-0.5,0.5},{0.5,0.5}}]},
 {(*FrTree*)MapIndexed[{Hue[0.022*#2[[1]],0.9,1,0.6],CapForm["Round"],Thickness[th*0.8^#2[[1]]],Line[#]}&,branches]},
 {(*Red Leaves*)MapIndexed[{Hue[0.03(*gen*),1,1,0.9],CapForm["Round"],Thickness[th*0.84^(gen+1)],Translate[Line[#],{2,0}]}&,Drop[branches,gen]]},
 (*Labels*)
 {Inset[Style[Text@TraditionalForm@Style[Row[{"Scaling Ratio r"," ""       "" Seed    z = ",y+x*I}],18],Gray],{0,-1.6}]},
 {Inset[Style[Text@TraditionalForm@Style[Row[{"r = |z|"," = ",SetAccuracy[Norm[{{pt1[[1]],0.5},{0,0}}],4],"                ",z," =    ",SetAccuracy[0.5,4]+SetAccuracy[pt1[[1]],4]I}],16],Gray],{0,-1.8}]},
 {Inset[Style[Text@TraditionalForm@Style[Row[{"Angle   \[Theta] = Arg(z)"," = ",SetAccuracy[VectorAngle[{pt1[[1]],0.5},{0,0.5}],4]," rad = ",SetAccuracy[180/Pi*VectorAngle[{pt1[[1]],0.5},{0,0.5}],2]"\[Degree]         "}],16],Gray],{0,-2}]},
{Inset[Style[Text@TraditionalForm@Style[Row[{"Hausdorff Dimension \!\(\*SubscriptBox[\(D\), \(H\)]\) = ",SetAccuracy[ Log[2]/Log[1/Norm[{{pt1[[1]],0.5},{0,0}}]],4]}],18],Gray],{2.3,-1.6}]},
{Inset[Style[Text@TraditionalForm@Style[Row[{"Leaves = ",Count[Drop[branches,gen],_Real,\[Infinity]]/4" ""     ""Length = ",SetAccuracy[Count[Drop[branches,gen],_Real,\[Infinity]]/4*(Norm[{{pt1[[1]],0.5},{0,0}}]^gen),3]}],18],Gray],{2.3,-1.8}]},
{Inset[Style[Text@TraditionalForm@Style[Row[{"Polynomial Trees       by Bernat Espigulé"}],18],Gray, Opacity[0.4]],{2.3,-2}]}},
PlotRange->{{-1.7,3.7},{-2.1,1.5}},ImageSize->{1000,600},Background->Black]],
{{th,0.025,"Thickness"},0.005,0.185},
{{gen,12,"Generations"},Range[1,16], ControlType -> SetterBar},
{{pt1,{0.5,0.5}},{-0.5,0.5},{0.5,0.5},Locator}]

Jurassic Trees Doodler


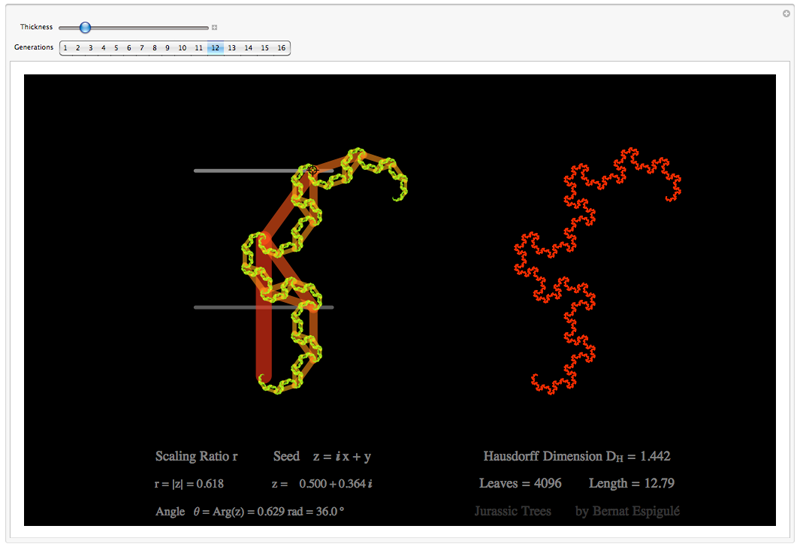
 Manipulate[
 Module[{branches=NestList[Flatten[Map[{{#[[2]],#[[2]]+{Reverse[{pt1[[1]],0.5}],{-1,1}*{pt1[[1]],0.5}}.(#[[2]]-#[[1]])},{#[[2]],#[[2]]+{Reverse[{pt1[[1]],-0.5}],{-1,1}*{pt1[[1]],-0.5}}.(#[[2]]-#[[1]])}}&,#],1]&,{{{0,-1},{0,0}}},gen]},
 Graphics[{{CapForm["Round"],Gray,Thickness[0.005],Opacity[0.7],Line[{{-0.5,-0.5},{0.5,-0.5}}]},{CapForm["Round"],Gray,Thickness[0.005],Line[{{-0.5,0.5},{0.5,0.5}}]},
 {(*FrTree*)MapIndexed[{Hue[0.022*#2[[1]],0.9,1,0.6],CapForm["Round"],Thickness[th*0.72^#2[[1]]],Line[#]}&,branches]},
 {(*Red Leaves*)MapIndexed[{Hue[0.03(*gen*),1,1,0.9],CapForm["Round"],Thickness[th*0.8^(gen+1)],Translate[Line[#],{2,0}]}&,Drop[branches,gen]]},
 (*Labels*)
 {Inset[Style[Text@TraditionalForm@Style[Row[{"Scaling Ratio r"," ""       "" Seed    z = ",y+x*I}],18],Gray],{0,-1.6}]},
 {Inset[Style[Text@TraditionalForm@Style[Row[{"r = |z|"," = ",SetAccuracy[Norm[{{pt1[[1]],0.5},{0,0}}],4],"                ",z," =    ",SetAccuracy[0.5,4]+SetAccuracy[pt1[[1]],4]I}],16],Gray],{0,-1.8}]},
 {Inset[Style[Text@TraditionalForm@Style[Row[{"Angle   \[Theta] = Arg(z)"," = ",SetAccuracy[VectorAngle[{pt1[[1]],0.5},{0,0.5}],4]," rad = ",SetAccuracy[180/Pi*VectorAngle[{pt1[[1]],0.5},{0,0.5}],2]"\[Degree]         "}],16],Gray],{0,-2}]},
{Inset[Style[Text@TraditionalForm@Style[Row[{"Hausdorff Dimension \!\(\*SubscriptBox[\(D\), \(H\)]\) = ",SetAccuracy[ Log[2]/Log[1/Norm[{{pt1[[1]],0.5},{0,0}}]],4]}],18],Gray],{2.3,-1.6}]},
{Inset[Style[Text@TraditionalForm@Style[Row[{"Leaves = ",Count[Drop[branches,gen],_Real,\[Infinity]]/4" ""     ""Length = ",SetAccuracy[Count[Drop[branches,gen],_Real,\[Infinity]]/4*(Norm[{{pt1[[1]],0.5},{0,0}}]^gen),3]}],18],Gray],{2.3,-1.8}]},
{Inset[Style[Text@TraditionalForm@Style[Row[{"Jurassic Trees       by Bernat Espigulé"}],18],Gray, Opacity[0.4]],{2.3,-2}]}},
PlotRange->{{-1.7,3.7},{-2.1,1.2}},ImageSize->{1000,600},Background->Black]],
{{th,0.03,"Thickness"},0.005,0.185},
{{gen,12,"Generations"},Range[1,16], ControlType -> SetterBar},
{{pt1,{0.5,0.5}},{-0.5,0.5},{0.5,0.5},Locator}]

As far as I know these four families of fractal trees have not been presented before so I’ve just uploaded them on a single CDF to the Demonstration Project. I will share with you its url when published.

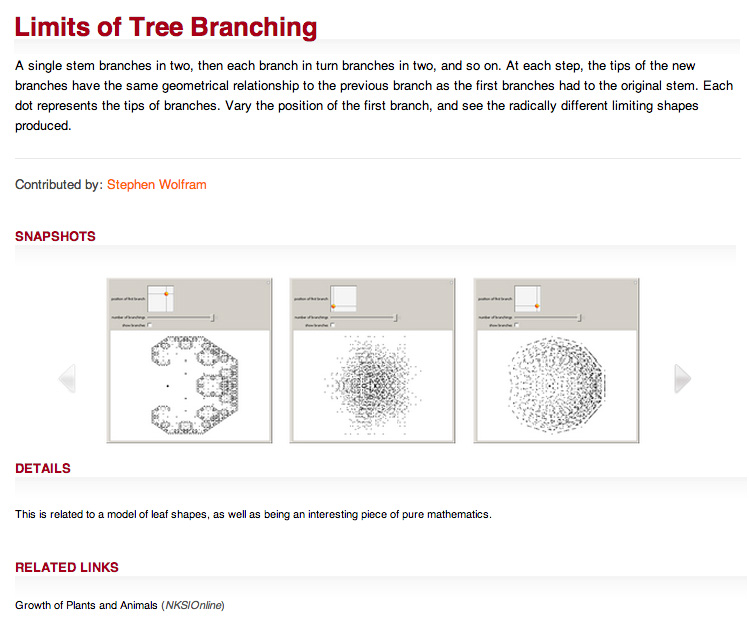
If you would like to explore other demonstrations dealing with these dragons here are the links to the “Paperfolding Dragon Curve” by Todd Rowland, the original Polynomial Trees by Michael Trott (check also his recent posts (1, 2, 3) about other creative ways of doodling in Mathematica ), and the classic “Limits of Tree Branching” by Stephen Wolfram.







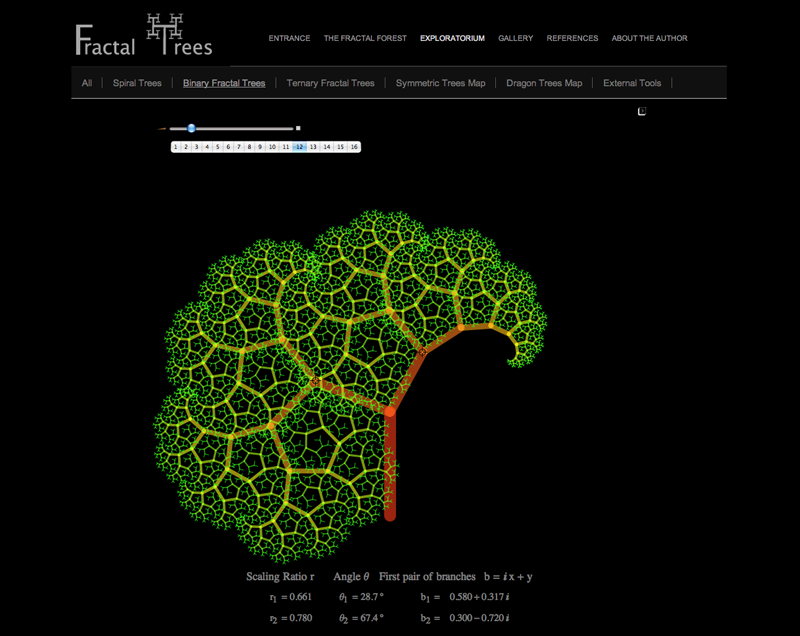
Finally, if you liked Theodore Gray’s “Tree Bender”, here you will find my adapted CDF for exploring binary trees with color and with meaningful parameters to describe them precisely.



That’s all for today! Enjoy, and let me know if you had been lucky enough to find a tree worthy of worship ;-). 
POSTED BY: Bernat Espigulé
1 Reply
Sort By:
I also found interesting the Journal Article example "Mandelbrot and Julia Fractal Sets" by Eric Weisstein; and Vitaliy's blog post "How to Make Interactive Apps with CDF" with his Random Tree Bender:
POSTED BY: Bernat Espigulé
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract