New THE MATHEMATICA JOURNAL article:

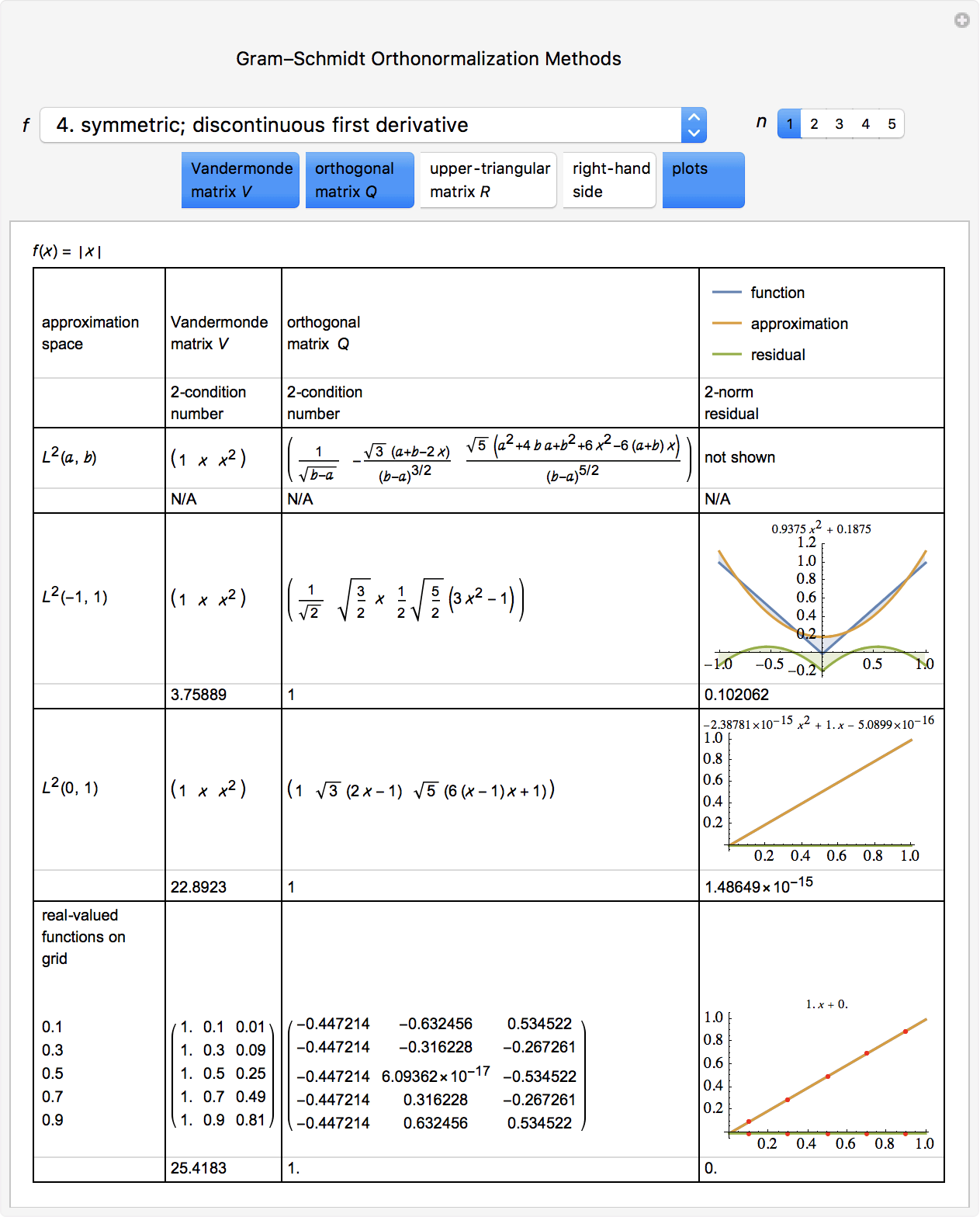
Polynomial $L^2$ Approximation

Relating Orthonormal Polynomials, Gram—Schmidt Orthonormalization, QR Factorization, Normal Equations and Vandermonde and Hilbert Matrices

by GOTTLOB GIENGER

ABSTRACT: This didactic synthesis compares three solution methods for polynomial $L^2$ approximation and systematically presents their common characteristics and their close interrelations:

1. Classical Gram–Schmidt orthonormalization and Fourier approximation in $L^2(a,b)$
2. Linear least-squares solution via QR factorization on an equally spaced grid in $[a,b]$
3. Linear least-squares solution via the normal equations method in $L^2(a,b)$ and on an equally spaced grid in $[a,b]$

The first two methods are linear least-squares systems with Vandermonde matrices $V$ ; the normal equations contain matrices of Hilbert type $H=V^TV$ . The solutions on equally spaced grids in $[a,b]$ converge to the solutions in $L^2(a,b)$. All solution characteristics and their relations are illustrated by symbolic or numeric examples and graphs.

• Read full text
• Submit an article