Message Boards Message Boards

Improvement on the magic number 0x5f3759df

One of the well-known algorithm of doing the inverse square root:

$$\frac{1}{\sqrt{x}}$$

is the so-called "fast inverse square root" algorithm, see wikipedia. This code gives a very good approximation of this function, possibly good enough for lighting in video-games. Even now, with modern CPUs, with many new instructions, this is still quite a bit faster than the actual inverse square root. The most surprising thing about this code is the appearance of a magic constant (note that this is C code, including the original comments)

float Q_rsqrt( float number )
{
    long i;
    float x2, y;
    const float threehalfs = 1.5F;

    x2 = number * 0.5F;
    y  = number;
    i  = * ( long * ) &y;                       // evil floating point bit level hacking
    i  = 0x5f3759df - ( i >> 1 );               // what the f*ck? 
    y  = * ( float * ) &i;
    y  = y * ( threehalfs - ( x2 * y * y ) );   // 1st iteration

    return y;
}

As you can see, the input is a float (a 32 bit floating point number), which is cast in to a long integer, the bits are shifted, and the result subtracted from a magic constant, this number is then re-interpreted again as a float.

To understand why this works is actually quite a long story, but realise that floats are stored as 32 bits as follows:

SEEEEEEEEMMMMMMMMMMMMMMMMMMMMMMM

where S= sign, E = exponent, and M = Mantissa. So once you interpret this as a long, and start shifted bits, you can get very unpredictable behavior. The question that I'm after is: can this constant be improved?

Let's create a library function in c and link it back in to Mathematica, such that we can try different magic constants and different values x:

Needs["CCompilerDriver`"]
src="
#include \"WolframLibrary.h\"
DLLEXPORT mint WolframLibrary_getVersion(){
  return WolframLibraryVersion;
}
DLLEXPORT int WolframLibrary_initialize( WolframLibraryData libData) {return 0;}
DLLEXPORT void WolframLibrary_uninitialize( WolframLibraryData libData) {return;}
DLLEXPORT int constantzero(WolframLibraryData libData, mint Argc, MArgument *Args, MArgument Res){
   MArgument_setInteger(Res, 0);
   return LIBRARY_NO_ERROR;
}
DLLEXPORT int fastinvsqrt(WolframLibraryData libData, mint Argc, MArgument *Args, MArgument Res) {
    double in = MArgument_getReal(Args[0]);
    int magic = MArgument_getInteger(Args[1]);
    float x = in;
    float halfx = 0.5f * x;
    int i = *(int*)&x;
    i = magic - (i >> 1); 
    x = *(float*)&i;
    x = x*(1.5f-(halfx*x*x));
    double I1; 
    I1 = x;
    MArgument_setReal(Res, I1);
    return LIBRARY_NO_ERROR;
}";
Quiet@LibraryFunctionUnload[fastinvsqrt]
fastinvsqrtlib=CreateLibrary[src,"fastinvsqrt"]
fastinvsqrt=LibraryFunctionLoad[fastinvsqrtlib, "fastinvsqrt",{Real,Integer},Real]
magicconst=16^^5f3759df
Plot[{1/Sqrt[x],fastinvsqrt[x,magicconst]},{x,0.1,5},PlotRange->{0,2}]
LogLogPlot[{1/Sqrt[x]-fastinvsqrt[x,magicconst],1/Sqrt[x]},{x,0.01,100000},PlotRange->{All,{10^-6,10}},Frame->True,PlotRangePadding->None,PlotPoints->1200,MaxRecursion->3]

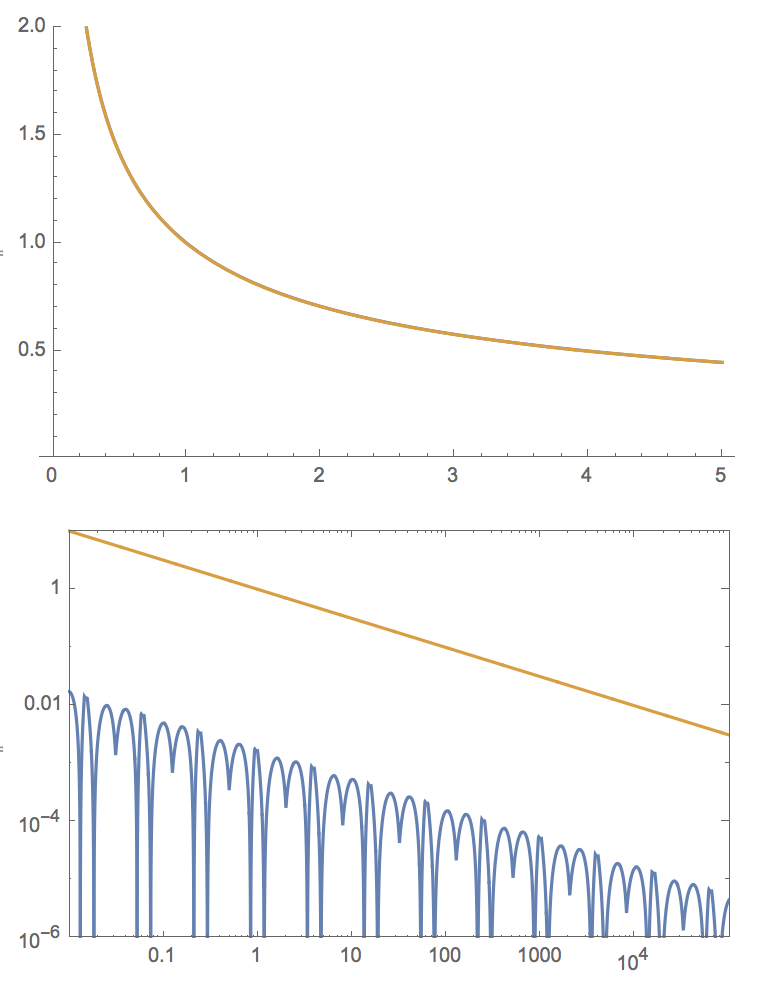
enter image description here

The match is indeed great! and we can see that the error (second plot, in blue) is of the order 0.1% of the result for the original magic constant!

Let's introduce the relative error:

ClearAll[relativeerror]
relativeerror[x_Real, magic_Integer] := (1/Sqrt[x] - fastinvsqrt[x, magic])/(1/Sqrt[x])

and plot it:

LogLogPlot[relativeerror[x, magicconst], {x, 0.01, 100000}, 
 Frame -> True, PlotRangePadding -> None, PlotRange -> {10^-5, 1}, 
 PlotPoints -> 1200, MaxRecursion -> 3]

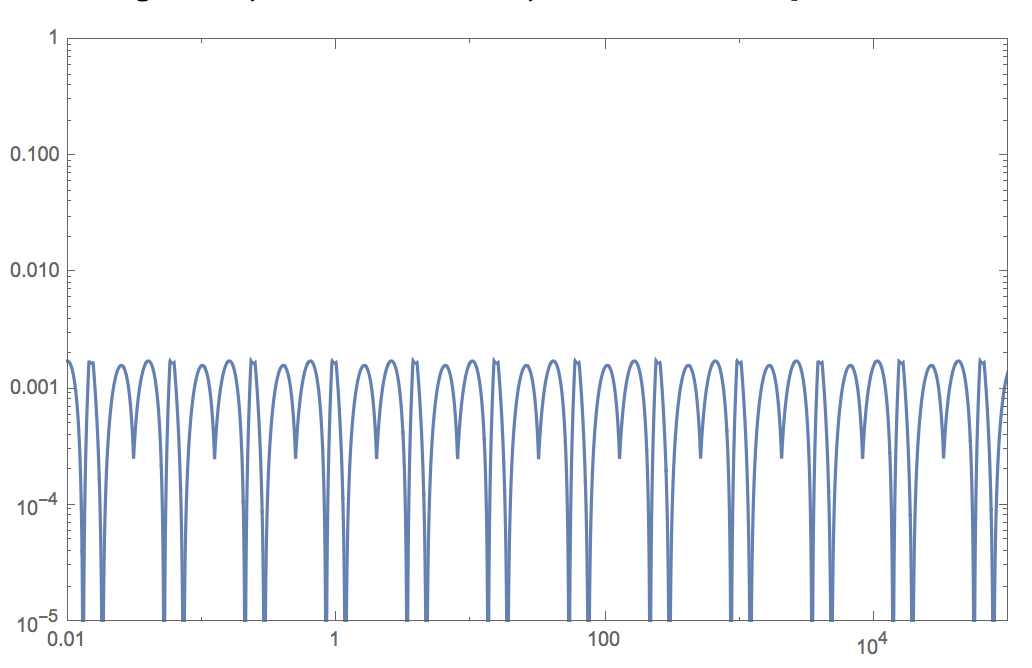
enter image description here

This plot is periodic because of the way floating point numbers are defined/implemented, we can zoom in on one of the parts:

LogLinearPlot[relativeerror[x, magicconst], {x, 1, 4}, Frame -> True, 
 PlotRangePadding -> None, PlotRange -> All, PlotPoints -> 1200, 
 MaxRecursion -> 3]

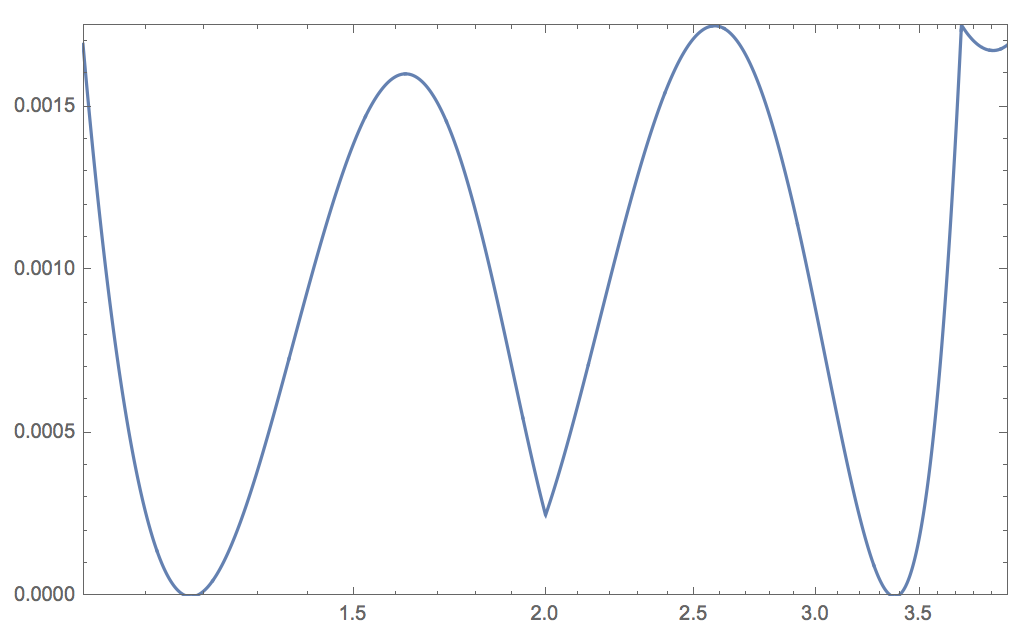
enter image description here

We can plot slight deviations from the magic constant to see the new relative errors:

LogLinearPlot[{relativeerror[x, magicconst], 
  relativeerror[x, magicconst - 20000], 
  relativeerror[x, magicconst + 20000]}, {x, 1, 4}, Frame -> True, 
 PlotRangePadding -> None, PlotRange -> All, PlotPoints -> 1200, 
 MaxRecursion -> 3, PlotLegends -> {"0", "-20000", "+20000"}]

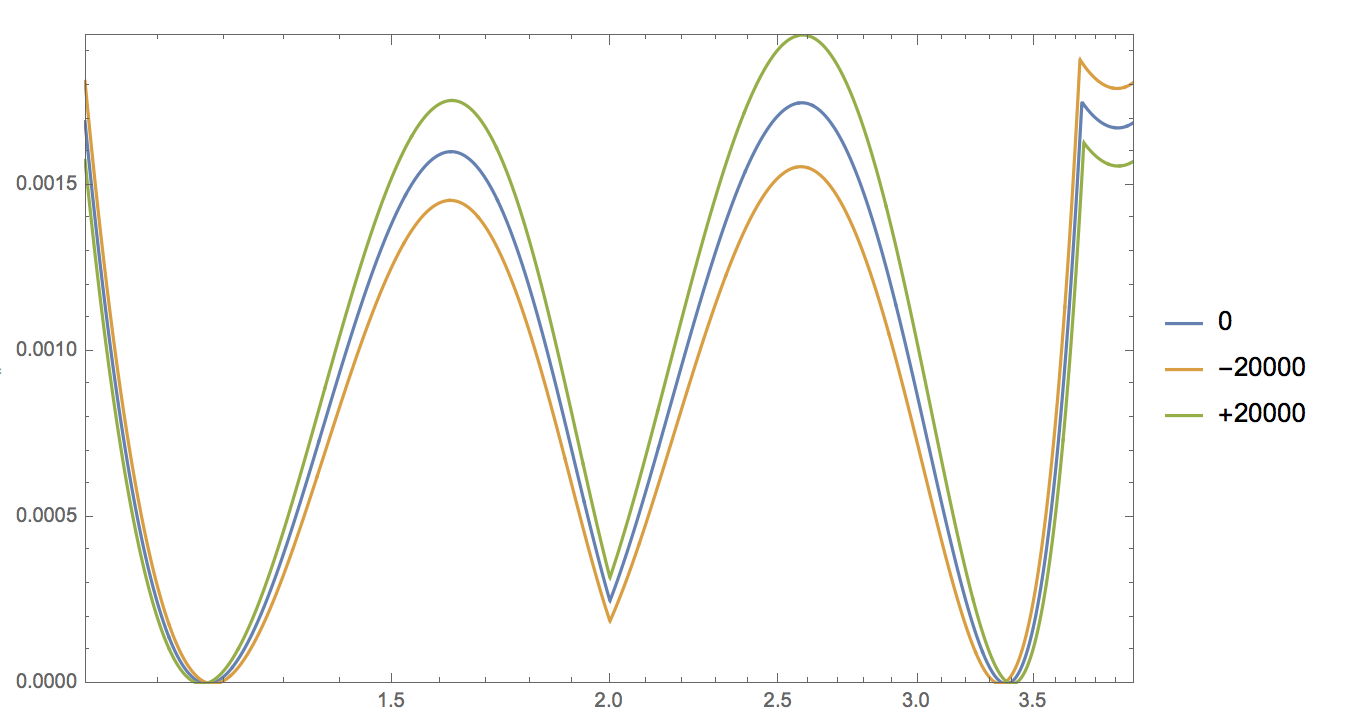
enter image description here

If the constant increases, the center peaks go up, but the far-right and far-left peak go down.

Let's try a bunch of magic-constants, and check the maximum (relative) error we find. I do this by sampling many point and looking for the maximum error I find in those points:

Dynamic[d]
data = Table[{d,  Max[Table[With[{x = 2^s}, ((1/Sqrt[x] - fastinvsqrt[x, d + magicconst])/(1/Sqrt[x]))], {s, 0, 2, 0.00001}]]}, {d, -100000, 100000, 
    1000}];
data // ListLogPlot
TakeSmallestBy[data, Last, 1]

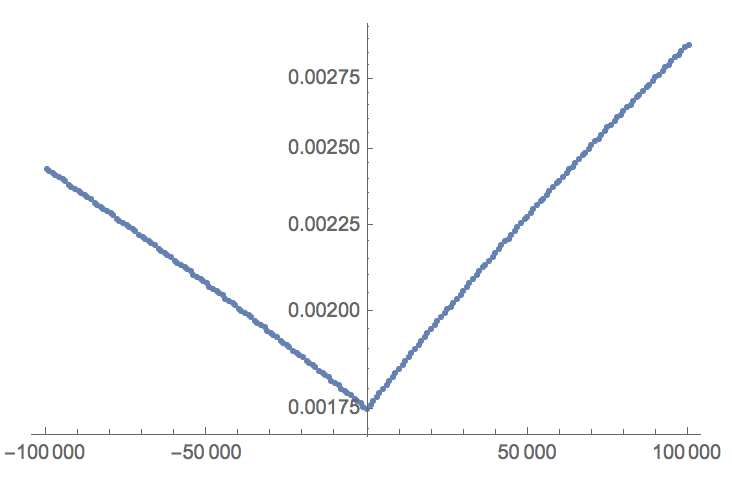
enter image description here

{{0, 0.00175225}}

If there is a better constant, it sure is close to the original constant. Let's zoom in a bit:

Dynamic[d]
data = Table[{d,  Max[Table[With[{x = 2^s}, ((1/Sqrt[x] - fastinvsqrt[x, d + magicconst])/(1/Sqrt[x]))], {s, 0, 2, 0.00001}]]}, {d, -1000, 1000, 10}];
data // ListLogPlot
TakeSmallestBy[data, Last, 1]

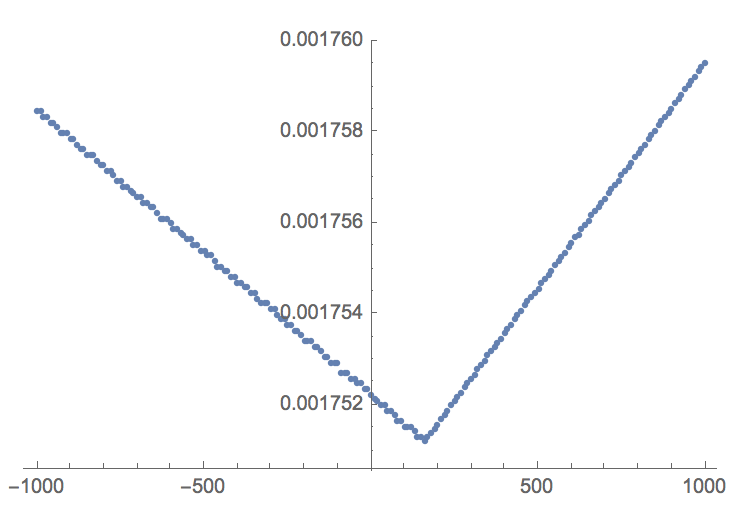
enter image description here

{{160, 0.00175121}}

We can zoom in even further:

Dynamic[d]
data=Table[{d,Max[Table[With[{x=2^s},((1/Sqrt[x]-fastinvsqrt[x,d+magicconst])/(1/Sqrt[x]))],{s,0,2,0.0000001}]]},{d,160,170,1}];
data//ListLogPlot
TakeSmallestBy[data,Last,1]

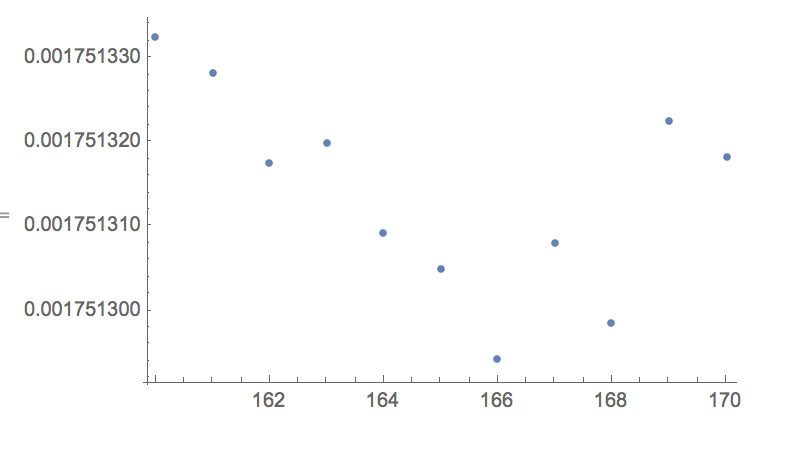
enter image description here

{{166, 0.00175129}}

magicconstant + 166 seems to have a slightly better worst-case performance. This corresponds to the follow new magic constant:

BaseForm[magicconst + 166, 16]

or in C (in hex):

0x5f375a85

We could also use the built-in FindMaximum:

ClearAll[FindMaxima]
FindMaxima[d_Integer]:=Module[{x},
    Max[Table[First@FindMaximum[((1/Sqrt[x]-fastinvsqrt[x,d+magicconst])/(1/Sqrt[x])),{x,x0,1,4},MaxIterations->5000,WorkingPrecision->50],{x0,1.0,4.0,0.03}]]
]

Now using this function and look around our probable minimum:

Dynamic[d]
data=Quiet@Table[{d,FindMaxima[d]},{d,150,175,1}];
data//ListLogPlot
TakeSmallestBy[data,Last,1]

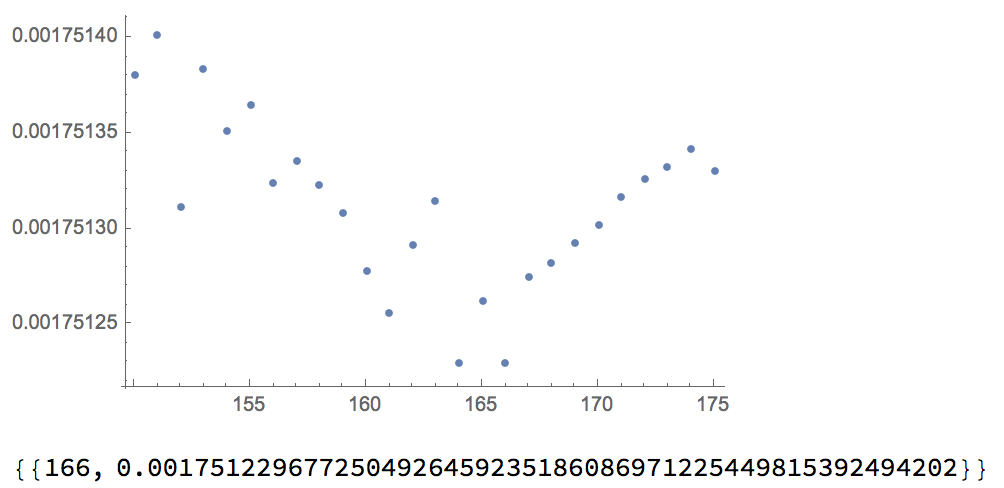
enter image description here

Which also find 166. So that seems to be in agreement. Another paper found 0x5f375a86 which 16^^5f375a86 - magicconst = 167. So perhaps he/me is wrong with rounding somehow…

Average error

So far, we've been looking at maximum error possible, but what about minimising the average error? Since we're using floating point numbers that can range over many many decades I would like to minimize the following integral of the error:

Integrate[relativeerror[2^s]^2,{s,0,2}]

Note that I do not sample the domain x 1 to 4 linearly. Again we can run for large deviations from the magic constant:

Dynamic[d]
data=Table[{d,Total[Table[With[{x=2^s},((1/Sqrt[x]-fastinvsqrt[x,d+magicconst])/(1/Sqrt[x]))^2],{s,0,2,0.00001}]]},{d,-250000,250000,10000}];
data//ListLogPlot
TakeSmallestBy[data,Last,1]

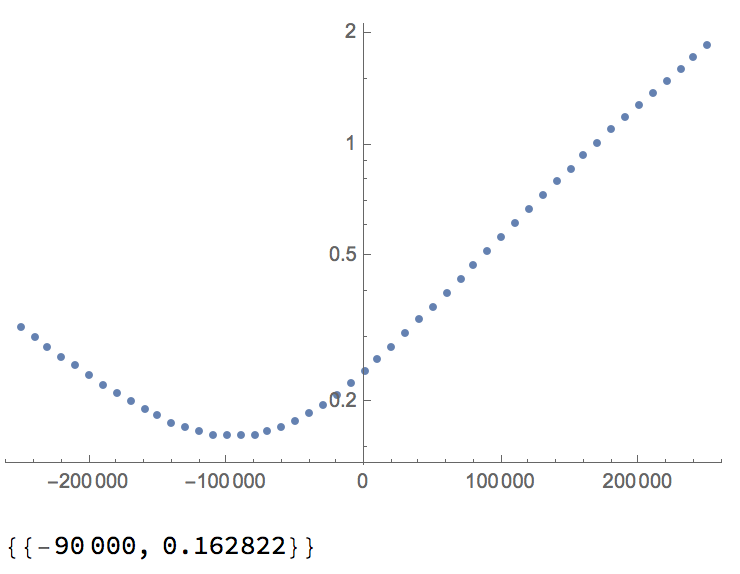
enter image description here

Let's zoom in a bit more:

Dynamic[d]
data=Table[{d,Total[Table[With[{x=2^s},((1/Sqrt[x]-fastinvsqrt[x,d+magicconst])/(1/Sqrt[x]))^2],{s,0,2,0.00001}]]},{d,-96000,-94000,20}];
data//ListLogPlot
TakeSmallestBy[data,Last,1]

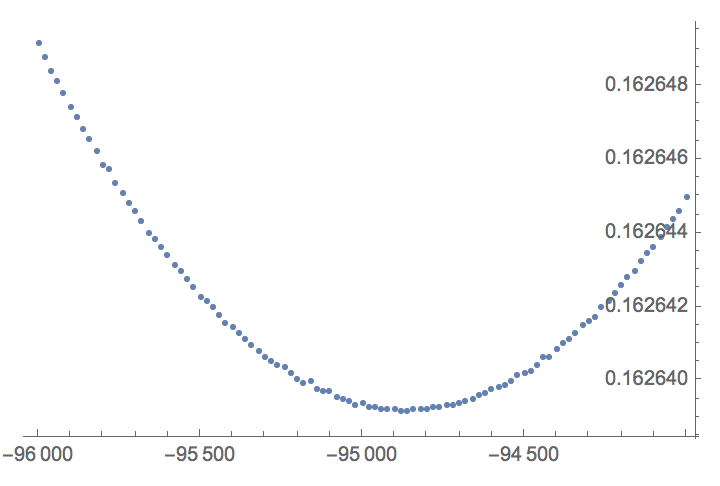
enter image description here

And zooming a bit more and using a smaller 'integration' steps:

Dynamic[d]
data=Table[{d,Total[Table[With[{x=2^s},((1/Sqrt[x]-fastinvsqrt[x,d+magicconst])/(1/Sqrt[x]))^2],{s,0,2,0.00000005}]]},{d,-94900,-94800,1}];
data[[All,2]]=Rescale[data[[All,2]]];
ListPlot[data,PlotRange->All]
TakeSmallestBy[data,Last,1]

enter image description here

The lowest value happens at magicconstant - 94863:

LogLogPlot[{relativeerror[x,magicconst],relativeerror[x,magicconst-94863]},{x,0.01,100000},Frame->True,PlotRangePadding->None,PlotRange->{10^-5,1},PlotPoints->1200,MaxRecursion->3]
LogLinearPlot[{relativeerror[x,magicconst]^2,relativeerror[x,magicconst-94863]^2},{x,1,4},Frame->True,PlotRangePadding->None,PlotRange->All,PlotPoints->1200,MaxRecursion->3]

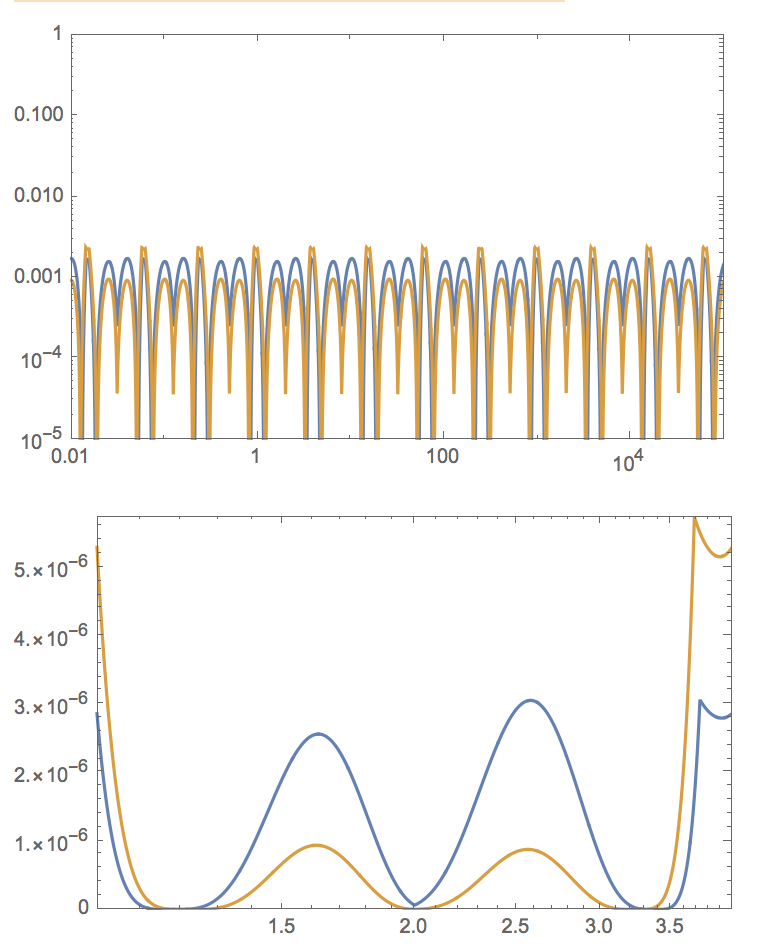
enter image description here

Here (in orange) the average (square) relative error is better as compared to the original constant.

Hope you enjoyed this little exploration of using C code inside Mathematica and to optimize low-level algorithms interactively using Mathematica's library functionality and plotting functionality. The original code includes a single Newton iteration to further hone in to the correct answer, the plots I've showed are for a single iteration. Other people have optimized the constant for not a single iteration or two iterations… So there are different constants out there. And, since the values are always under-estimated, the Newton iteration can also be modified to account for this.

POSTED BY: Sander Huisman
3 Replies
Sort By:

enter image description here - Congratulations! This post is now a Staff Pick! Thank you for your wonderful contributions. Please, keep them coming!
POSTED BY: EDITORIAL BOARD

Thanks for the functions in Wolfram language! I stayed away from doing it in Wolfram because sometimes it 'catches' computations with very small/big numbers and convert it automatically to arbitrary precision, moreover, I wanted to play a bit with library-linking c code. But your functions seem to work fine! Thanks for sharing! Arrayplot is a good way of visualizing what happens.

You're indeed right! 'most of the work' is done by shifting the exponent part of the number. The algorithm can actually be generalised for any exponent between -1 and 1, see also discussion here. Perhaps, as a follow up, I will compute the magic constant as a function of the power…

POSTED BY: Sander Huisman

Thanks for posting this, Sander.

There are other examples of bit hacks and I have always wondered whether others are out there waiting to be discovered. Here there is the possibility of long range effects due to carrying. More wild possibilities come from multiplication, of course counting on the conventions for overflow, as well as the integer encoding. The thinking from Wolfram's "A New Kind of Science" is relevant, and probably his methods as well.

Before I get too off topic, here are some definitions to explore this wholly within Wolfram Language:

magicconst = 16^^5f3759df;
FloatBitsToReal[list_] := 
 N[(-1)^list[[1]] 2^(FromDigits[list[[2 ;; 9]], 2] - 127) FromDigits[
     Prepend[list[[10 ;;]], 1], 2]/2^23];
RealToFloatBits[x_] := Join[{Sign[x] /. {1 -> 0, -1 -> 1}},
    IntegerDigits[#[[2]] + 126, 2, 8], Rest[#[[1]]]] &[
  RealDigits[x, 2, 24]];

and the C code then becomes

InvSqrt[x_] := Module[{i, x2, y},
  x2 = .5 x;
  y = x;
  i = FromDigits[RealToFloatBits[y], 2];
  i = magicconst - BitShiftRight[i, 1];
  y = FloatBitsToReal[IntegerDigits[i, 2, 32]];
  y*(1.5 - (x2*y*y))]

Here is an ArrayPlot where the first row is the magicconstant, the second row is the float for 1.2, then it is shifted to the right, and the last row is the subtraction from the magic constant.

steps in fast inv sqrt

I guess the reason why this works is that the base 2 exponent is effectively multiplied by -1/2 which serves as a pretty good approximation to x^(-1/2) no matter what happens to the mantissa. Simplifying the search for a magic constant to a manageable size, (akin to the NKS methodology) by looking for alternatives with the exponent part, we can just look at 8 bits.

MinimalBy[Range[0, 255], 
Function[m, 
Sum[Total[
IntegerDigits[
BitXor[127 - Quotient[i - 127, 2], m - BitShiftRight[i, 1]], 
2]], {i, 0, 255}]]] (* {190, 191}*)

ArrayPlot[IntegerDigits[{190, 191}, 2, 9], Mesh -> True]

bits in 190 and 191

So (unless I made a mistake) there are two possibilities for the exponent part. The magic constant corresponds to 190. Maybe there is a better magic constant with the bits from 191?
POSTED BY: Todd Rowland
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract