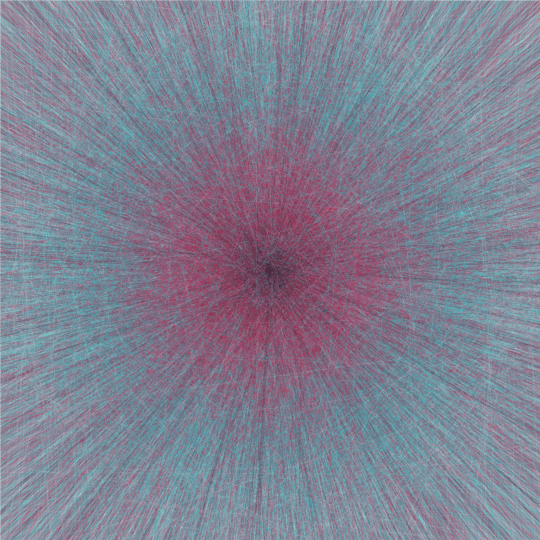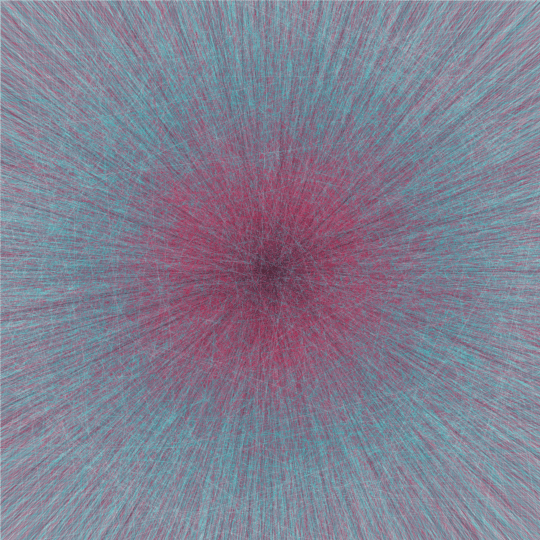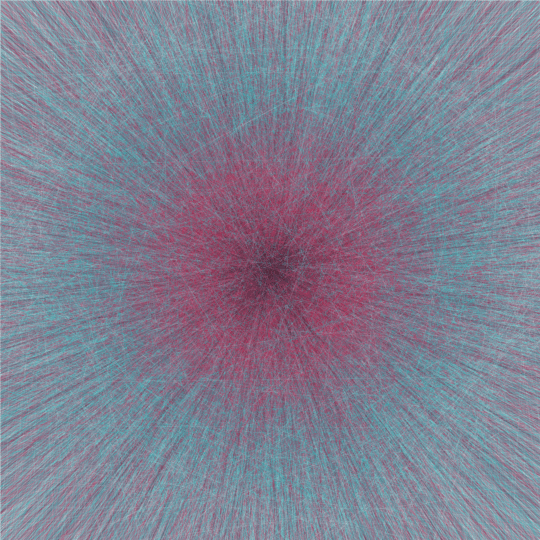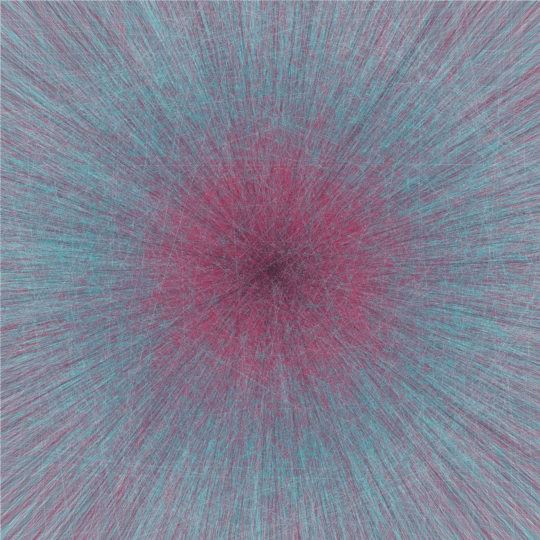
Random Lines
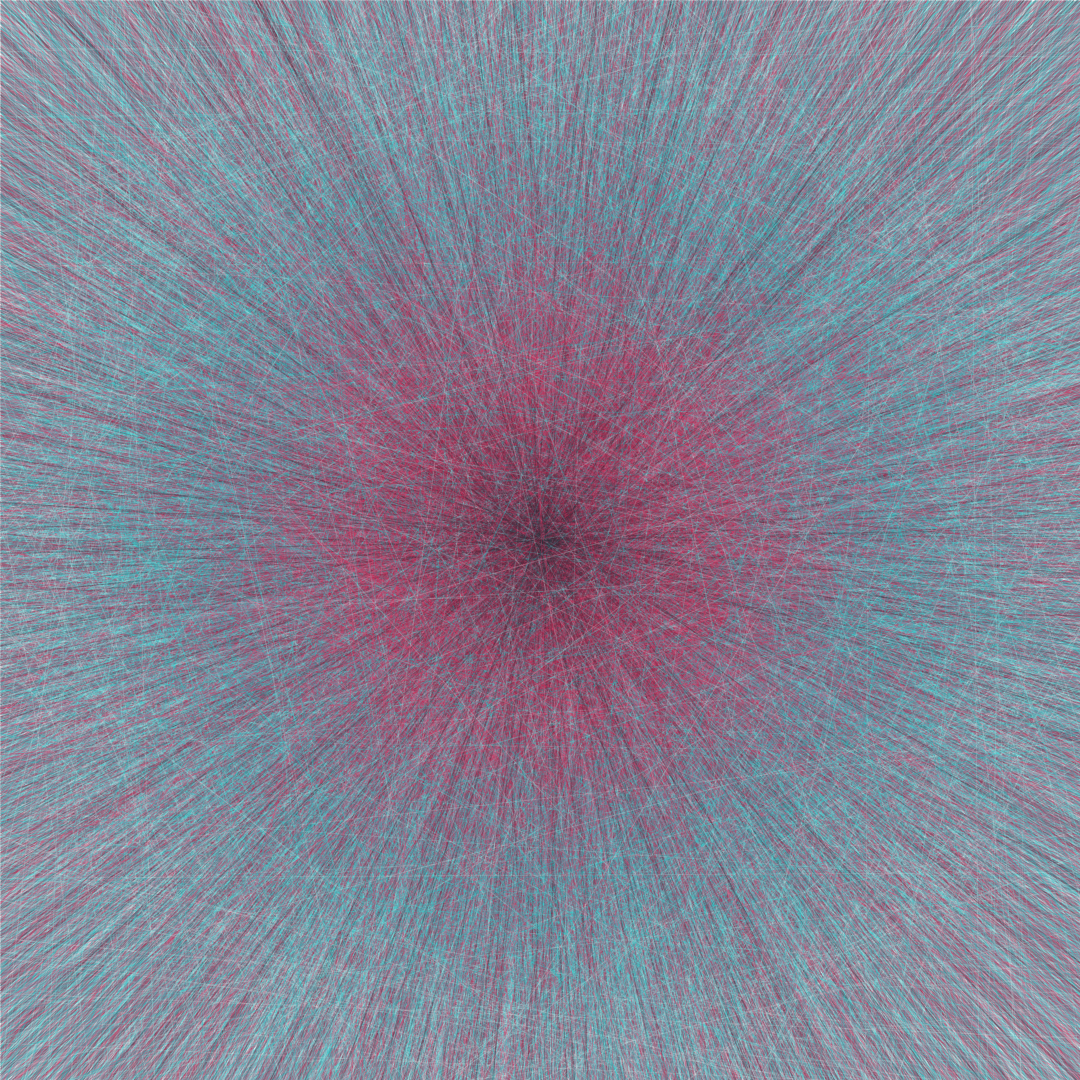
This animation consists of 8 frames, each of which contains 20,000 randomly chosen lines. The frames are completely independent of each other, but they're each generated by the same basic process, so they look fairly similar.
In each case I generate 20,000 independent random points in the unit disk and 20,000 independent random directions, and then draw a line through each point parallel to the corresponding direction. The lines are colored according to the distance of the point to the origin: those passing through a chosen point close to the origin are nearly black, and then as the chosen point gets further out the color cycles through a reddish-pink, a turquoise, and then finally a light gray.
In order to generate the points, I choose the radius $r$ uniformly on $[0,1]$ and the angle $\theta$ uniformly on $[0,2\pi]$; then the point is $(r \cos \theta, r \sin \theta)$. (Note that these points are not uniform in the unit disk: they are concentrated near the origin. I'm choosing $r$ in this way just because I like how the resulting image looks better than for uniform points in the disk.)
The frames in the animation are independent, so I just generated 8 of them and then concatenated them into a single GIF. Here's the code to generate a single frame with width and height dimensions both doubled, followed by an example frame:
RandomAngle[] := RandomVariate[UniformDistribution[{0, 2 Pi}]];
RandomDirection[] := With[{θ = RandomAngle[]},
{Cos[θ], Sin[θ]}
];
Module[{r, θ, v, p, cols = RGBColor /@ {"#252A34", "#FF2E63", "#08D9D6", "#EAEAEA"}},
Graphics[{Thickness[.0002],
Table[{
r = RandomVariate[UniformDistribution[]];
θ = RandomAngle[];
v = RandomDirection[];
p = {r Cos[θ], r Sin[θ]};
{Blend[cols, r], InfiniteLine[p, v]}},
{20000}]},
PlotRange -> 1, ImageSize -> 1080]
]