Gif inspired by beesandbombs.

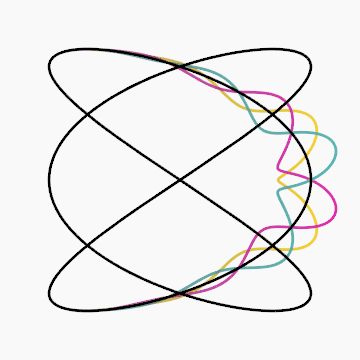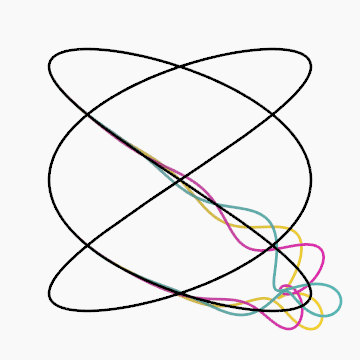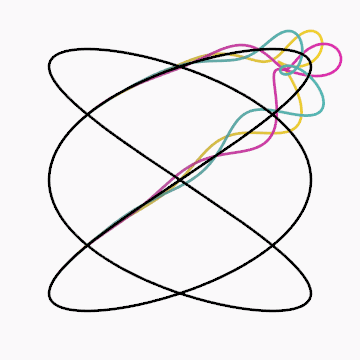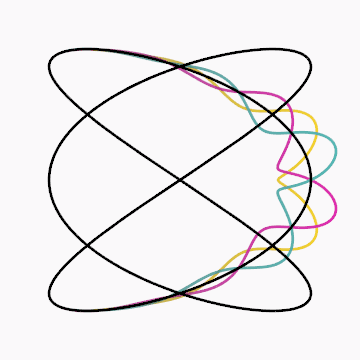
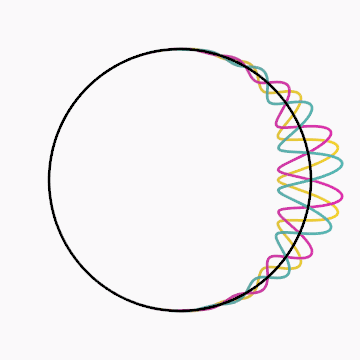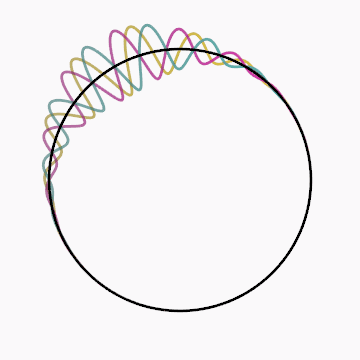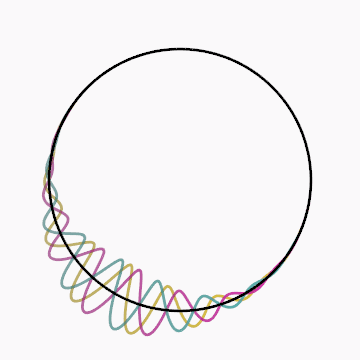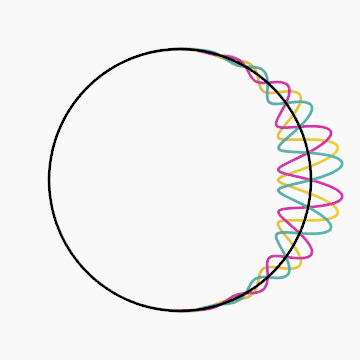
Code:

DynamicModule[{\[Sigma] = (2*Pi)/25, r, f, \[Phi], P},
 r[t_] := 8 {Cos[3 t], Sin[2 t]};
 f[t_, t0_, \[Phi]_] := Exp[-((t - t0)^2/(2 \[Sigma]^2))] Cos[17 t - \[Phi]] 2;
 P[t0_, \[Phi]_, c_] := ParametricPlot[If[\[Phi] == -1, r[t], r[t] + {-1, 1} f[t, t0, \[Phi]] Reverse@Normalize[r'[t]]],
   {t, -Pi + t0, Pi + t0}, PlotRange -> 11 {{-1, 1}, {-1, 1}}, 
   Axes -> False, PlotStyle -> Thickness[0.008],
   ColorFunction -> If[\[Phi] == -1, Black &, (Blend[{{-1.5, Transparent}, {1, RGBColor@c}}, #] &)], Background -> RGBColor@"#FAF9FA"];
 res = Manipulate[
   Show@{P[t0, 0, "#F2D12E"], P[t0, Pi/2, "#DE2DAE"], 
     P[t0, 3 Pi/2, "#55B7B4"], P[t0, -1, Black]}
   , {t0, 0, 2 Pi, 0.1}]
 ]