Introduction

In courses as Physical Chemistry or Quantum Mechanics, Chemistry and Physics major students learn about solving Schrodinger’s equation for systems from 1 to 3 dimensions. Analytical solutions for these systems are not always easy to obtain, and the traditional computational methods used to get numerical solutions are difficult to implement at the undergraduate level. The students are restricted to the simplest systems and must trust or believe in the solutions displayed in the textbooks. The development of interactive tools to teach Quantum Mechanics using Wolfram Language, and in particular the functionalities NDEigensystem and Manipulate, would offer sophisticated and powerful learning tools to the undergrads. The student would have an active role in the learning process, for example, having the chance to inquire on the effects on the wave functions when the potential energy is changed.

This project aims to develop interactive learning tools based on Wolfram Language for a third year undergraduate physical chemistry course. The learning tool will concentrate on quantum systems of chemical interest such as the hydrogen molecular ion, the 3-dimensional harmonic oscillator, and the rigid molecular rotor. This learning tool must be design thinking on future developments or extensions to include more complex systems of interest in advanced undergraduate courses like quantum chemistry or molecular spectroscopy.

Written Content / Lesson Plans

Quantum Chemistry/Mathematica, QC/M, is a course planned to teach the foundations and applications of quantum mechanics in chemistry by using Wolfram Language. The first third of QC/M will give an introduction to classical and quantum mechanics, the second part of the course introduces the application of quantum mechanics to atoms and molecules. The final third will deal with modern applications like quantum dynamics in chemistry and molecular spectroscopy. Although this seems an ambitious course for a third year undergraduate chemistry major, this course will relies upon the student's background in Mathematics, Physics and the use of Wolfram Language to compute wave functions.

This notebook will cover the introduction to atomic and molecular orbitals by using Mathematica to compute the electronic wave function for Hydrogen and Hydrogen molecule ion. Students will have the opportunity to learn by inquiring into the notebook content and instructions. They could learn about the relation between the solutions of Schrödinger's equation and the physical constrains imposed on molecular systems. The content of this notebook is:

1. Hamiltonian Operator for the Coulomb potential: central force

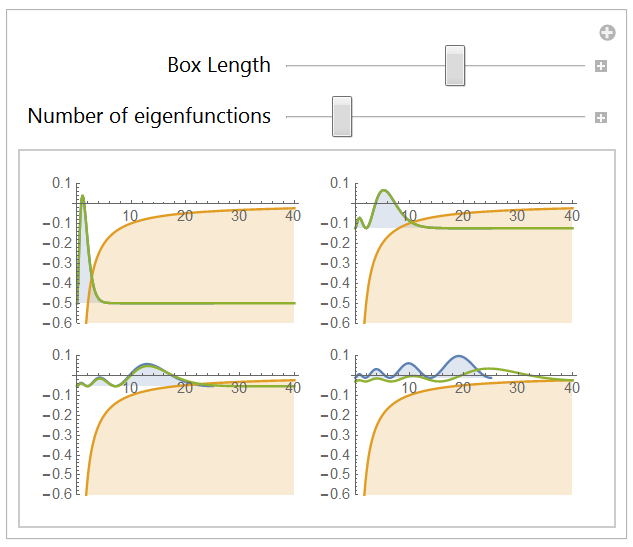
2. The 1-dimension Hydrogen atom

   2.1 Boundary conditions

   2.2 Eigenstates

   2.3 Computing the lowest energy eigenstates

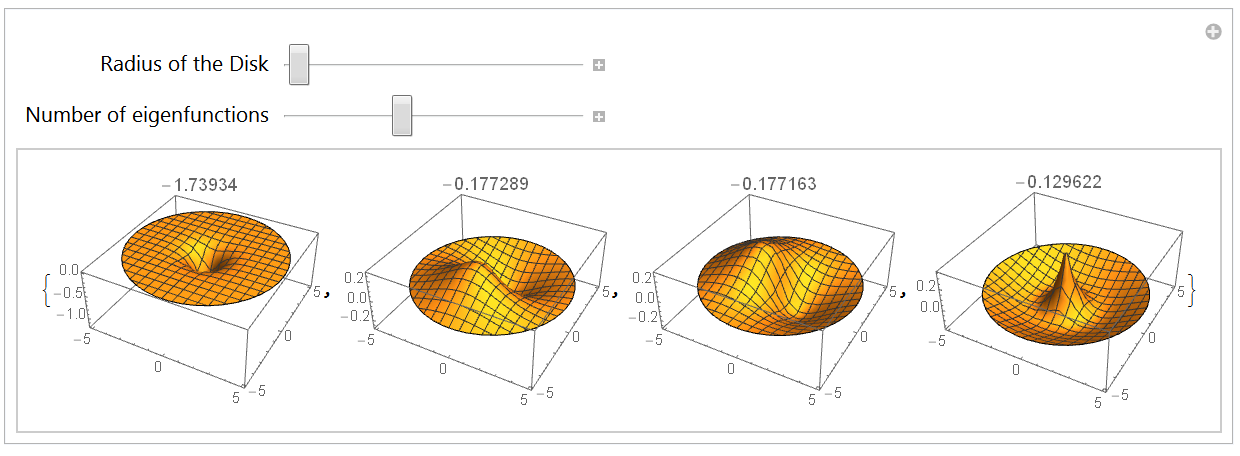
3. The 2-dimensional Hydrogen atom

   3.1 Boundary conditions and integration region

   3.2 Eigensystem with annular integration region

   3.3 Eigensystem with a disk-like integration region

   3.4 The potential energy surface and the ground state

4. The 1-dimension hydrogen molecule ion: H2+

   4.1 Hamiltonian: regularization of the Coulomb potential

   4.2 Eigensystem

   4.3 Born-Oppenheimer curves

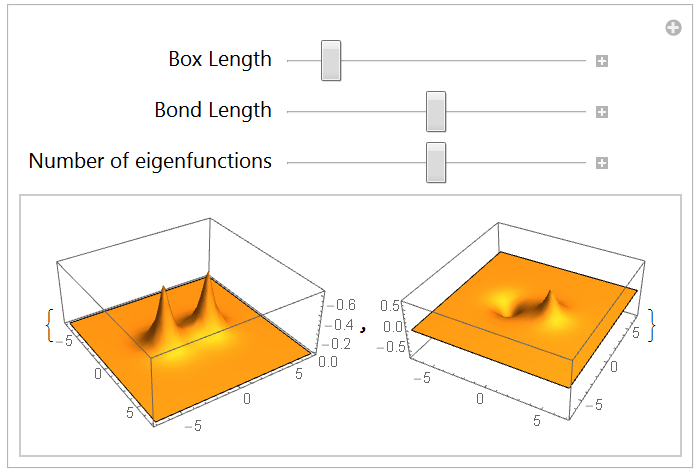
5. The 2-dimensional hydrogen molecule ion: H2+

   5.1 Redefining the Hamiltonian: List and Sequence

   5.2 Eigensystem and lowest energy states

Code

QS1e.nb: Use of NDEigensystem and Manipulate to study 1-electron systems

Highlights

Conclusion

This notebook will be used in the quantum chemistry course during the fall-2017 semester. The Hydrogen atom and the Hydrogen molecular ion are of fundamental importance to understand the principles of the chemical bonding. The concept of atomic or molecular orbital is not clearly understood for many chemistry undergraduate students, and probably a reason for this is the passive role of students in typical quantum chemistry lectures. The student can use this notebook to make/do real quantum chemistry, in an active way, by computing orbitals of atoms and molecules. The elaboration of this notebook took approximately two weeks, but there is still some work to be done for the realistic 3-dimensional Hydrogen atom and molecule ion. This is enough class material to cover 3 weeks of the 16 weeks academic semester. As a professor and researcher in the field of theoretical and quantum chemistry, I am convinced of the importance for the students of learning to do molecular simulations. Chemistry has moved from studying proportion laws and stoichiometry to the formation and destruction of single chemical bonds. Theoretical tools as computer simulations give a first insight and a direct molecular description of chemical reactions, therefore a computational thinking is of central importance to learn not only quantum chemistry but chemistry in general. It is my expectation that this initiative could be extended to courses of Physics and Mathematics at Universidad Icesi in Cali - Colombia.

Future Directions

1. The structure of functions and the notebook will allow straightforward extensions to 2 - electron and/or 3 - dimension systems.

2. The inclusion of a kinetic energy operator for the nuclei will allow to deal with systems with strong nuclear-electronic correlation.

3. Enrich the content of this notebook with contextualization about the use of quantum mechanics in chemistry.

4. Solve the 1-dimensional Hydrogen molecule ion with multiple domains connected through boundaries by requiring continuity of the electron wave function and its derivative.

References

[1] Moss, R. E., "The Hydrogen atom in one dimension", Am. J. Phys. 55, 397, 1987

[2] Palma, G., Ulrich R., "The one-dimensional hydrogen atom revisited", Canadian Journal of Physics, 84(9): 787-800, 2006

[3] Loudon, R, "One-dimensional hydrogen atom", Proc. R. Soc. A, 472 20150534, 2016

[4] Yang, X. L., Guo, S.H., Chan, F. T., Wong, K. W., Ching, W. Y., "Analytical solution of a two-dimensional hydrogen atom. I. Nonrelativistic theory", Phys. Rev. A, 43, 1186, 1991

[5] Hasoun, G. Q., "Two-particle 1-dimensional model of the Hydrogen molecular ion in an ultrashort laser pulse", Am. J. Phys. 49 (2), 143, 1981

[6] Duan, Y, Yin, M., An, W., He, C., "A one-dimensional Model of Hydrogen Molecular Ion", Commun. Theor. Phys. (Beijing, China), 31, 27-32, 1999

[7] Dutta, S. Shreemoyee, G., Dutta-Roy, B., "A cartoon in one dimension of the hydrogen molecular ion", European Journal of Physics 29, 235, 2008

[8] Patil, S. H. "Hydrogen molecular ion and molecule in two dimensions" J. Chem. Phys. 118, 2197, 2003