Introduction

I'm a 15 year old student that this year has had the privilege to attend the Wolfram Summer Camp and created, helped by my mentor Greg "Chip" Hurst, a visualization of the results of extending tetration (aka power towers) to different realms. In the following post I will go over the basics of tetration and its properties and then how we expanded it to different number sets.

The basics of tetration

Tetration is, long story short, repeated powers. You have a base "a" and a height "h" and the result of "a tetrate t" is simply $a^{a^{a^{a..}}}$(h times). To understand it better we can compare it to other arithmetic operations:

Multiplication is repeated addition: a*b = a+a+a+a+...+a (b times)
Exponentiation is repeated multiplication: a^b = a*a*a*a*...*a (b times)
Tetration is repeated powers: a^a^(a...)(b times)

Although there are many different ways of representing tetration the most common one is $$^{z} a$$. One of the most important properties of tetration that should always stay true is the fact that $$^{n} a = a^{\left({^{n-1} a}\right)}$$.

Implementing basic tetration into Mathematica should be easy:

Tetration[a_, k_Integer] := Power @@ Table[a, {k}]
Tetration[2, 3]

16

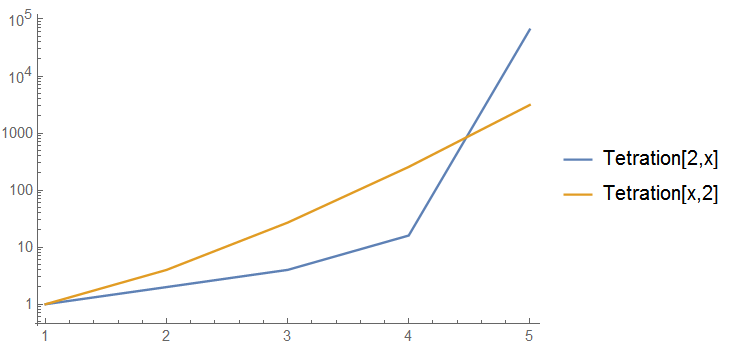
We can also plot the results:

ListLogPlot[{Table[Tetration[2, x], {x, 0, 4}], 
  Table[Tetration[x, 2], {x, 1, 5}]}, PlotRange -> All, 
 Joined -> True, PlotLegends -> {"Tetration[2,x]", "Tetration[x,2]"}]

The Challenge: Extending tetration to other realms

- Complex base, ? height

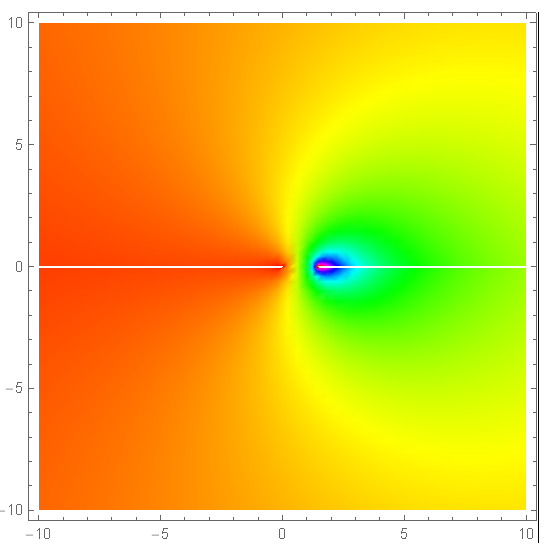
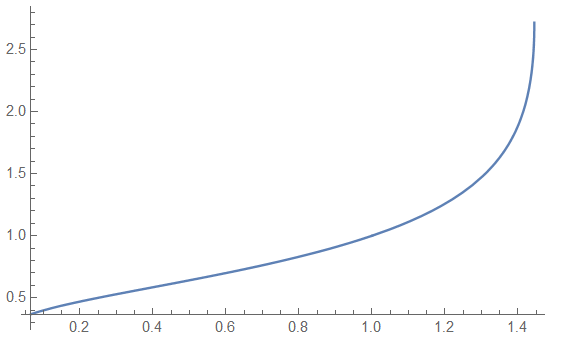
Let h(z) be $z^{z^{z^{z..}}}$(? times). Now take logarithms both sides resulting in $z^{z^{z^{z..}}} = h(z) \log z = \log h(z)$. Solving for $h(z)$ results in the limit of the function which, as proven by Euler, converges for $\exp(-e) < x < \exp(1/e)$: $h(z) = - W(-\log z)/\log z$ where $W(x)$ is the principal branch of the W Lambert Function which describes the product of logarithms. In Mathematica, such function is called ProductLog[x]. We can plot $h(a)$ for different complex $a$ or for its convergence interval:

h[z_] = -(ProductLog[-Log[z]]/Log[z]);
DensityPlot[Abs[h[x + (I*y)]], {x, -10, 10}, {y, -10, 10}, 
 PlotRange -> All, ColorFunction -> Hue, PlotPoints -> 150]

Plot[h[x], {x, Exp[-E], Exp[1/E]}]

- Complex base, real height

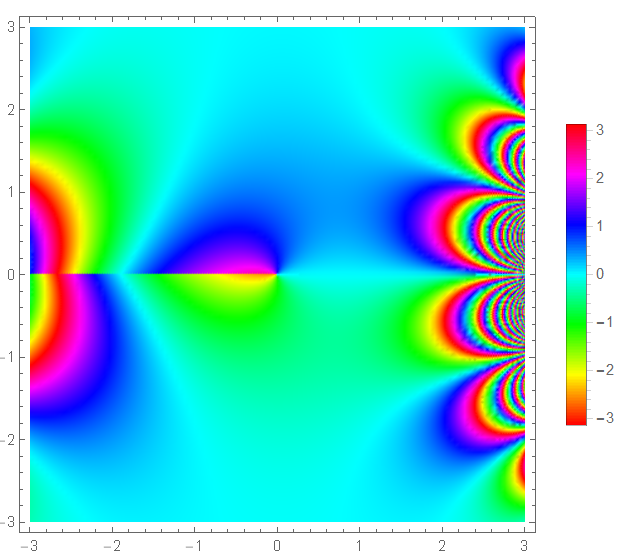
Although we couldn't find a graphic approximation to real-height tetration, a linear approximation we determined would be the best approach to visualize the problem. This linear approximation follows this piecewise function

Tetration[z_, x_Real] := 
  Piecewise[{{Log[z, tetrf[z, x + 1]], 
     x <= -1}, {1 + x, -1 < x <= 0}, {z^tetrf[z, x - 1], x > 0}}];

Fixing the height to (x = ?) and plotting on the height, attending to the argument of the base, results in:

- Complex base, complex height

According to the following source (https://mathoverflow.net/questions/259278/an-explicit-series-representation-for-the-analytic-tetration-with-complex-height/259371), there is a series analytical representation for complex height tetration. It uses the q-Pochhammer symbol and q Binomials.

The $q$-Pochhammer symbol: $$(p;\,q)_\infty = \prod_{k=0}^\infty(1-p\,q^k$$ $$(p;\,q)_z = \frac{(p;\,q)_\infty}{(p\,q^z;\,q)_\infty}, \quad z\in\mathbb C$$ $$(p;\,q)_n = \prod_{k=0}^{n-1}(1-p\,q^k), \quad n\in\mathbb N$$

The $q$-binomial coefficients: $${r \brack s}_q = \frac{(q;\,q)_r}{(q;\,q)_s \, (q;\,q)_{r-s}}.$$

Series: $$t(z) = \sum_{n=0}^\infty \sum_{k=0}^n (-1)^{n-k} \, q^{\binom {n-k} 2} {z \brack n}_q {n \brack k}_q ({^k a}).$$

Technically, this series only converges and can therefore have a meaningful value in the interval $-2 < \Re(z)$. However, we created a conjecture by which were able to - meaningfully - extend this interval to $\Re(z) <= -2$ by recursion (until it enters the "convergent" zone). Following the main property of tetration $$^{z} a = a^{\left({^{z-1} a}\right)}$$ we can also deduct $$^{z+1} a = a^{\left({^z a}\right)}$$ . Taking logarithms both sides we end up with $$log_a (^{z+1} a)= ^{z} a$$. After $\lceil -\Re(z) \rceil - 2+1$ iterations, it will jump to the original series.

Tetration[a_, z_ /; Re[z] <= -2] := Log[a, tet[a, z + 1]];

So, the handle-all-cases function would end up being:

ClearAll[Tetration, qBinomial];
Options[Tetration] = {"Terms" -> 4, WorkingPrecision -> 30};
qBinomial[args__] := qBinomial[args] = QBinomial[args];
Tetration[_, -1, ___] = 0;
Tetration[a_, n_Integer /; n >= 0, o___] := 
  Tetration[a, n, o] = 
   Block[{$MaxExtraPrecision = 10000, $IterationLimit = 10000}, 
    Power @@ Table[a, {n}]];
Tetration[a_(*/;1<a<E^(1/E)*), z_ /; Re[z] > -2, OptionsPattern[]] := 
  Block[{$MaxExtraPrecision = 10000, $IterationLimit = 10000}, 
   With[{q = -ProductLog[-Log[a]]}, 
    With[{limit =(*NumericalMath`NSequenceLimit@*)
       N[Total[Table[
          Sum[(-1)^(n + k) q^Binomial[n - k, 2] qBinomial[z, n, 
             q] qBinomial[n, k, q] Tetration[a, k], {k, 0, n}], {n, 0,
            OptionValue["Terms"]}]], OptionValue[WorkingPrecision]]}, 
     SetPrecision[limit, 3/4 Precision[limit]]]]];
Tetration[a_, z_, o___] /; Re[z] <= -2 := 
  Log[a, Tetration[a, z + 1, o]];

This code is an adapted version of the code posted here, posted by the author of the MSO question linked above. Plotting it...

Plot3D[Arg[
  Tetration[Log[3], SetPrecision [x + (I*y), \[Infinity]]]], {x, -4, 
  4}, {y, -4, 4}, PlotPoints -> 40, WorkingPrecision -> 60, 
 ColorFunction -> Hue, PlotLegends -> Automatic,  PlotRange -> All]

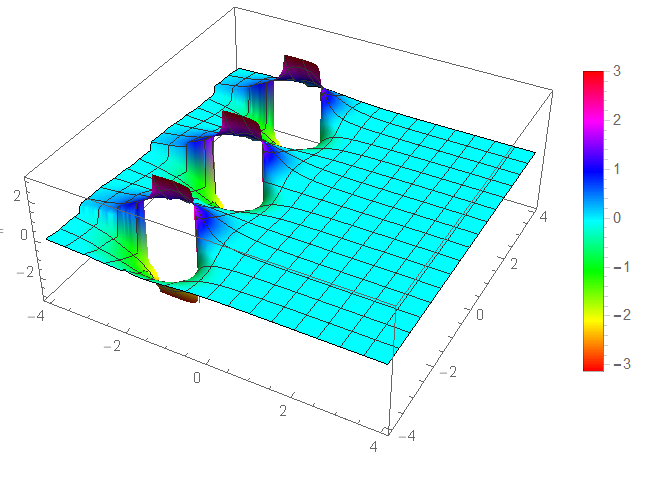
A bit of a counter-intuitive "property" of tetration and higher-order operations (pentation, hexation,...):

As we can see by plotting both functions, these are clearly not the same...

LogPlot[{x^x, x}, {x, 1, 9}, 
 PlotLegends -> {"y = \!\(\*FractionBox[\(Log[x]\), \
\(ProductLog[Log[x]]\)]\)", "y = x" }]