Hello! My name is Stephanie Nam, and my project was created at Wolfram Summer Camp 2017. This project allows for translations in the following languages: Burmese, English, and Korean. Also, it provides translations of numerals in Burmese, Hindu-Arabic, and Thai. Here is a link to the microsite of my project! https://www.wolframcloud.com/objects/stepha789/numeralSystems

Process

My project's first focus was to translate numbers in written Korean form to Hindu-Arabic numerals.

I first created an Association Thread which established a set of rules for the main function to go off of.

 newAssoc = <|"?" -> 0, "?" -> 1, "?" -> 2, "?" -> 3, "?" -> 4, 
      "?" -> 5, "?" -> 6, "?" -> 7, "?" -> 8, "?" -> 9, "?" -> 10, 
      "?" -> 100, "?" -> 1000, "?" -> 10000, "?" -> 100000000, 
      "?" -> 1000000000000|>

Then, I created a function that would translate characters to the numbers that they are defined as.

newKoreanChar[kor_String] :=
 newAssoc[#] & /@ (Characters[StringJoin[StringSplit[kor]]])

Lastly, after analyzing a pattern where the character's values would give the numeral form, I wrote a function that would provide the Hindu-Arabic numerals.

roughfunc4[koreword_List] :=
 Total[koreword //.
   {{before___, x_, y : Except[10000 | 100000000 | 1000000000000], 
       after___} /; x < y :> {before, x*y, after},
    {before___, z__, base1 : (10000), after___} /; 
      Max[z] < base1 :> {before, Plus[z]*base1, after},
    {before___, q__, base2 : (100000000), after___} /; 
      Max[q] < base2 :> {before, Plus[q]*base2, after},
    {before__, base3 : (1000000000000), after___} /; 
      Max[before] < base3 :> {Plus[before]*base3, after}}]

Extension

After finishing the functions for Korean to Hindu-Arabic numerals, I decided to also include the Burmese and Thai numeral systems in my project. Burmese numerals were used in the past in Myanmar while Thai numerals are still used in Thailand alongside the Arabic system.The functions for the translation of these systems and a microsite is in the attached file.

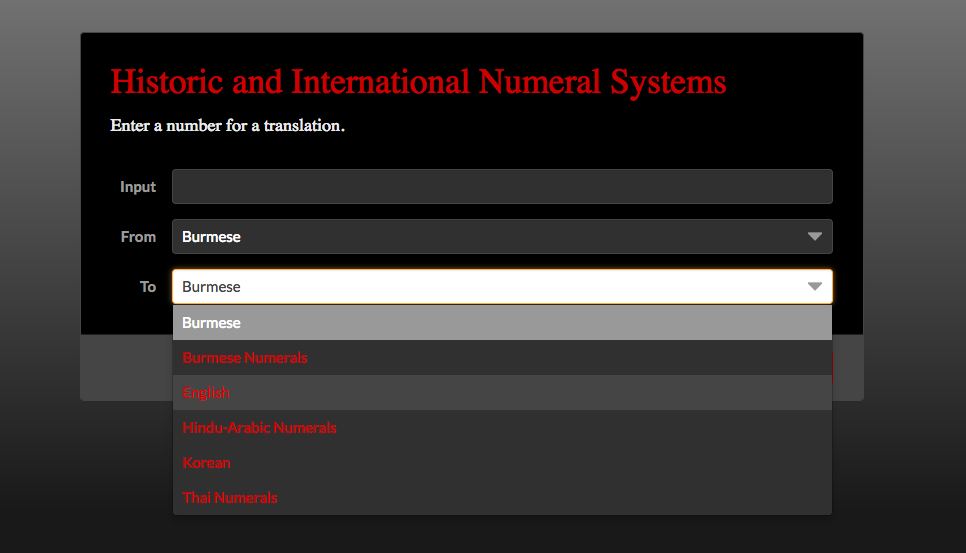
Conclusion

While working on this project, I was able to study the differences in structuring numbers for each numeral system. Furthermore, I was able to study how some languages created written forms of numbers with different bases of magnitude. For example, the number (10,000,000) is understood as 10 one-millions in English but identified as 1,000 ten-thousands in Korean. Also, in the Burmese language, an extra syllable is added to numbers that are not divisible by their place value. This rule can be seen in 21 where a marking is made and 20 which does not have a marking because it is divisible by its placeholder, ten. With these as well as other numeral systems many more differences can be analyzed!

Attachments: