Optimal circle packing is a very simple problem if all circles are a uniform radius. A hexagonal packing gives a density of $\frac{1}{6}\pi\sqrt{3} = 0.9068996821...$ However, if the circles are not all the same size, it is not clear whether a repeating tight packing is possible. It is also not clear whether packings with multiple sizes of circles will be more or less dense than a uniform packing. I attempted to answer these questions using an iterated packing algorithm.

Setup

Disjoint circles were randomly placed with a random choice of two radii. Several examples are pictured.

Algorithms

One possible algorithm to iteratively pack the circles is to simply move each circle a given amount closer to a specified center point, if doing so would not cause an overlap between circles. Though it does bring the circles closer together, this algorithm does not tightly pack the circles, because the circles do not move toward open spaces, only toward a center point, which leaves large open areas. This is clearly evident in the animation below.

The code for this algorithm is shown below.

compress[circles_, force_, dim_: 2] := 
     Module[
        {output = sortcircles[circles], temp},
        Do[
           temp = force *Table[5, dim] + (1 - force) output[[1, i]];
           If[RegionDisjoint[Ball[temp, output[[2, i]]], 
           Delete[output, {{1, i}, {2, i}}]], output[[1, i]] = temp];,
       {i, Length[circles[[1]]]}];
     output]

A smarter algorithm should consider relative positions of circles to each other, rather than only considering their positions relative to a center point. One way to achieve this is to triangulate the center points of all circles, and locate which lines between circles are especially long. Then, one or both of these circles can be moved toward the other in order to shorten the line. This algorithm tends to space out the circles evenly as they are being packed, resulting in a tighter packing. The following animation shows the process of repeatedly shortening the 70 longest lines in a triangulation of 50 circles. The triangulation of circles is shown in order to help visualize what the algorithm is doing.

This algorithm clearly results in a more dense packing of the unevenly sized circles

The code for this algorithm is shown below

shortenhalfline[circles_, twocirclesindecies_, force_, dim_: 2] := 
 Block[
  {pts = circles[[1]], output, twocurrentpts, currentpt, i, 
   temp},
  output = circles;
  twocurrentpts = Table[pts[[x]], {x, Flatten[twocirclesindecies]}];
  currentpt = 
   MaximalBy[twocurrentpts, EuclideanDistance[Table[5, dim], #] &][[1]];
  i = Position[twocurrentpts, currentpt][[1, 1]];
  temp = (force) Mean[twocurrentpts] + (1 - force) currentpt;
  output[[1, twocirclesindecies[[i, 1]] ]] = temp;
  If[! checkdisjoint[output, twocirclesindecies[[i, 1]]],
   output[[1, twocirclesindecies[[i, 1]] ]] = currentpt];
  output]

Results and Analysis

The second algorithm gives relatively tight packings of unevenly sized circles. It often produces packings with densities of 60 to 70 percent. It seems unlikely that packings with multiple sized circles will yield a density higher than uniformly sized circles using this method. Regular patterns generally do not emerge between different sized circles. However, it is common for areas of a single size size of circle will form a hexagonal pattern, as shown below.

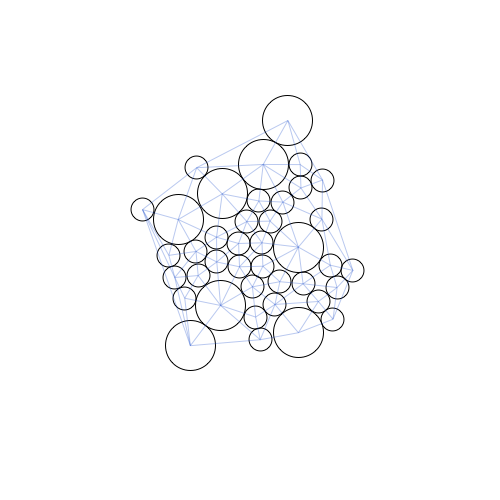
Algorithms like this tend to be successful at packing circles near the inside of the region, but circles near the outside do not always fit into the packing very tightly.

Ultimately, iteration of randomly placed and sized circles is unlikely to produce an optimal packing. However, It does offer insight into how dense an optimal non-uniform packing could be in comparison to a uniform one, and what this packing might look like.

Attachments: