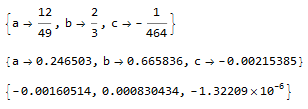As a physicist, I cringe when I see errors with so many significant figures.
I usually fit my data and use it as input for another simulation (in another program). I could interpolate the result, but this leads to bad derivatives. I could simply fit it and use the fit result, but it has so many significant figures and this makes the final expression barely readable...
One approach I found interesting it is to rationalize the parameters give the given error. This leads to nicer looking expressions. The code is as follows:
RationalizeModel[model_FittedModel, n_: 2] := Thread[
model["BestFitParameters"][[All,1]] -> (Rationalize[#1, #2/n] & @@@ model["ParameterTableEntries"][[All, {1, 2}]])]
Usage would be:
data = Table[{x, 1/4 Cos[2/3 x]} + RandomReal[{-1, 1}/50, 2], {x, 0, 2 Pi, 2 Pi/100}];
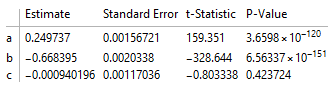
model = NonlinearModelFit[data, a Cos[b x] + c, {a, b, c}, x, Method -> NMinimize]
model["ParameterTable"]
A = RationalizeModel[model]
B = model["BestFitParameters"]
A[[All, 2]] - B[[All, 2]] (* Errror *)