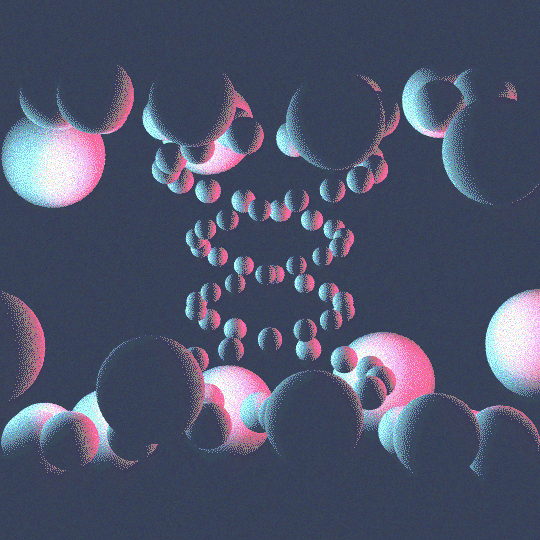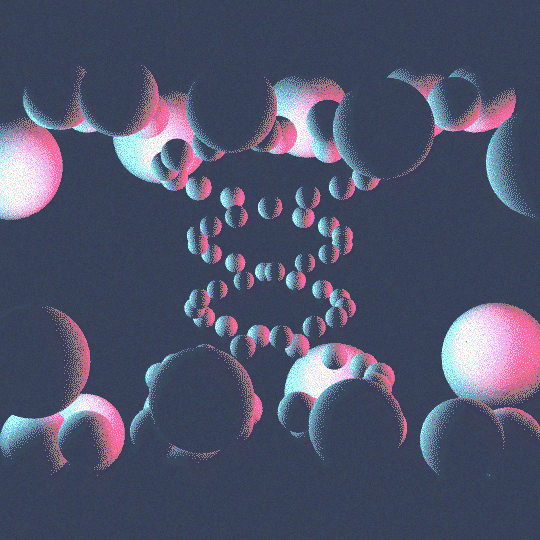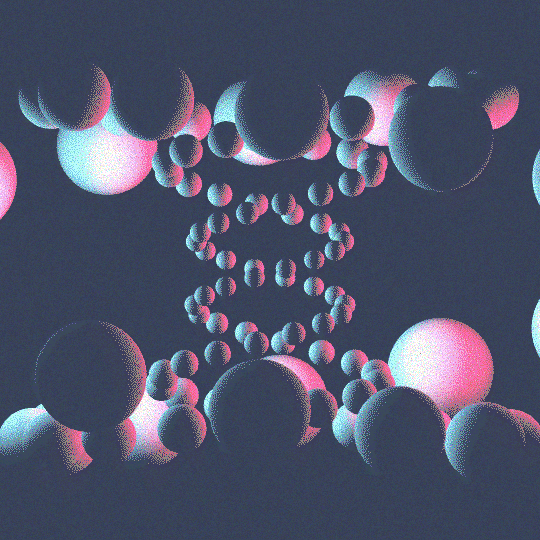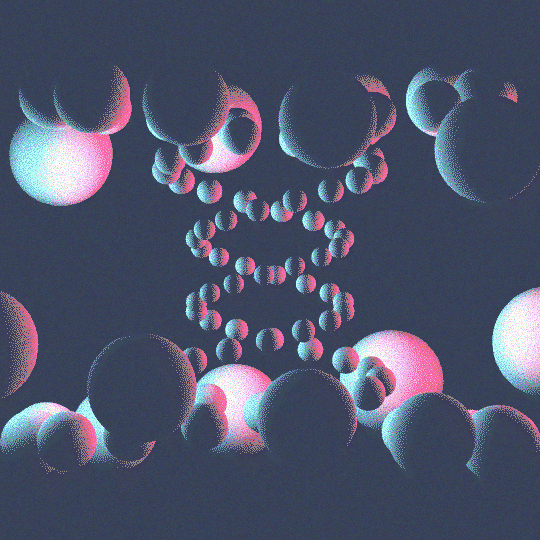
Septafoil

This is the same idea as Intertwine, but with the septafoil knot $7_1$ rather than the trefoil knot. Read the post on Intertwine for more details on the code, which is mostly identical. The one notable change is that I've added noise to each of the frames in the animation. This is accomplished by creating a single noisy image of the right size:

noise = ImageEffect[Graphics[Background -> None, ImageSize -> 540], {"PoissonNoise", .4}];

and then combining it with each frame using ImageMultiply. Also, after exporting I reduced the color palette to 40 colors and dithered the frames using gifsicle.

Here's the rest of the code (as with Intertwine, I used MaxRecursion -> 5 for the final export, but this is too computationally intensive to use inside Manipulate):

Stereo3D[{x1_, y1_, x2_, y2_}] := {x1/(1 - y2), y1/(1 - y2), x2/(1 - y2)};

pqtorus[t_, ?_, p_, q_] := 1/Sqrt[2] Flatten[ReIm /@ {E^(p I (t + ?/p)), E^(q I t)}];

DynamicModule[{p = 7, q = 2, n = 50, 
  viewpoint = 10. {Cos[-4 ?/5], Sin[-4 ?/5], 0}, point, basis,
   sphere, cols = RGBColor /@ {"#7AC7C4", "#F73859", "#384259"}},
 point[t_, ?_] := pqtorus[t + ?, 0, p, q];
 basis[t_, ?_] := NullSpace[{point[t, ?]}];
 sphere[t_, ?_, ?_, ?_] := 
  Cos[.1] point[t, ?] + Sin[.1] Total[{Cos[?] Sin[?], Sin[?] Sin[?], Cos[?]}*basis[t, ?]];
 Manipulate[
  ImageMultiply[
   ParametricPlot3D[
    Evaluate@
     Table[Stereo3D[sphere[t, ?, ?, ?]], {t, 0., 2 ? - 2 ?/(q n), 2 ?/(q n)}],
    {?, 0, ?}, {?, 0, 2 ?},
    Mesh -> None, PlotRange -> 4, ViewPoint -> viewpoint, 
    ViewAngle -> ?/80, ImageSize -> 540, Boxed -> False, 
    PlotStyle -> White, ViewVertical -> {0, 0, 1}, Axes -> None, 
    Background -> cols[[-1]],
    Lighting -> {{"Point", cols[[1]], 2 {Cos[7 ?/10], Sin[7 ?/10], 0}}, 
       {"Point", cols[[2]], 2 {Cos[17 ?/10], Sin[17 ?/10], 0}} , 
       {"Ambient", cols[[-1]], viewpoint}}],
   noise],
  {?, 0, 2 ?/(q n)}]
 ]