I get lots of error messages. I do not look at many of them. Sometimes I consider myself lucky to get an error message, since I also often get no message and no desired output.
I usually just go to the code to see if I can figure out what is confusing Mma.
I am hoping one of the experts here can expose the meaning of this one. This is from an example in the Mathematica Navigator book. Here's the example:
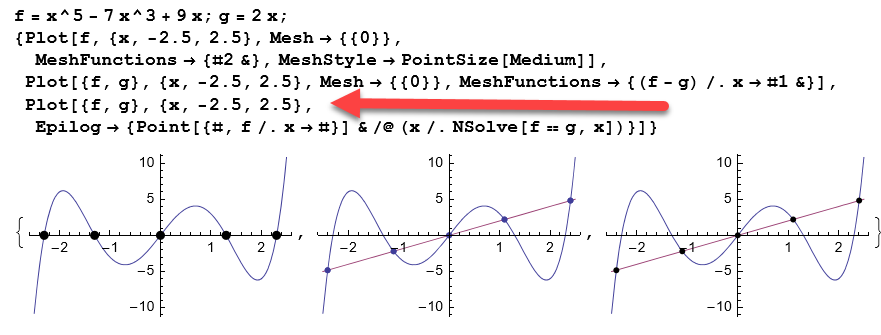
Here's my (intentionally slight) change.
f0[x_] := x^5 - 7 x^3 + 9 x (* was f = x^5 - 7 x^3 + 9 x *)
g0[q_] := 2 q (* was g = 2 x *)
Plot[{f0, g0}, {x, -2.5, 2.5}
, Epilog -> {Point[{#, f0 /. x -> #}] & /@ (x /.
NSolve[f0 == g0, x])}]
The error message is: HoldForm is not a Graphics primitive or directive.
Huh??
Needless to say I did not code HoldForm[]. I did find this HoldForm[] command in the output of FullForm[]: (output snipped due to volume).
So my questions is/are:
Q: Is this related to SetDelayed[]?
I was able to debug this one. A working version is:
Plot[{f0[x], g0[x]}, {x, -2.5, 2.5}
, Epilog -> {Point[{#, f0[x] /. x -> #}] & /@ (x /.
NSolve[f0[x] == g0[x], x])}]
Q: Does the corrected code help me relate the error message to the incorrect code?
Thanks in advance.