Hello,

my recent calculations have resulted in what's a new type of equation for me, and I'm completely confused as to how to solve it. I haven't dealt with anything "above" PDEs, and this being not an integral equation and not even an integro-differential equation, but a partial integro-differential equation - well, let's just say I don't know how to proceed. Here's the equation itself, with u(x,t) the function to be solved for:

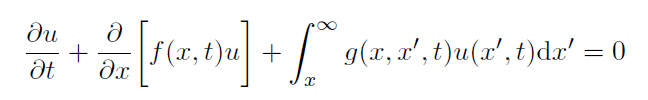
where the two functions f and g are both known but also quite complicated (each is defined numerically at least in some part, just to visualize this: it takes about 5 seconds to plot f(x,t) as a function of x with t held constant). This sort of makes me doubt that this kind of equation can be solved without some sort of high-end programming wizardry. As for the integral - the integrand is expected to drop relatively quickly with x', so that the integral does converge. Instead of the infinity, though, you can imagine some constant X which would encompass the bulk of the integrand. Finally, I should say there's an initial condition u(x,0)=h(x), with h(x) a known function. This initial condition should be sufficient without any boundary conditions, based on the physics the equation represents.

I have to say, I'm not a programming person at all (it's why I use Mathematica, it's quite user-friendly), and thus I would appreciate if the answer to this could be encapsulated in the form of Mathematica's functions, such as NDSolve. I've already tried using that one, but my kernel automatically reset itself without warnings after about a minute. Memory isn't the issue, though.

Thanks in advance!