
My students practice some math skills through interactive apps I develop. Feng Shui, for instance, helps them gain proficiency with function composition. I made a Wolfram Language version of Feng Shui. The results seemed interesting enough to share on this list.
The user clicks on the cover art and then answers six randomly generated function composition questions. The app tracks stats and reports a score at the end based on speed, accuracy, and difficulty of the questions. A score of 8000 indicates proficiency. Top scores are over 9000.
I've provided the full code below. To make it work, copy the attached FengShuiCover.jpg into where the code says
coverPic=
Then evaluate the code. To start, click on the cover art. When the math question appears, click once anywhere in the interface and start typing an answer. When you have typed a correct answer, you will automatically advance to another question.
Wolfram Advantage: In the Wolfram Language, Feng Shui's code shrunk to about a quarter of its HTML/JavaScript/PHP size, partly because of Wolfram's compact syntax and partly because Wolfram can handle math much more efficiently. For instance, to recognize a correct answer, JavaScript has to compare several variations of a polynomial (4x^2 9x + 1, 1 9x + 4x^2, etc) to what the user has typed, while Wolfram just compares the underlying symbolic expressions once.
Typing Math: I feel strongly that end users should not have to know some arcane set of key strokes to type math. In Feng Shui, the user types 4x^2-3x+1 but sees the following appear as she types:
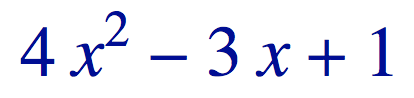
To accomplish this, I reduced the string that the user typed to characters and replaced some patterns of characters with boxes (e.g., SuperscriptBox[] or StyleBox[]). This simple example Italicizes x:
Characters[resp] /. "x" -> StyleBox["x", FontSlant -> Italic]
I have been able to extend this method in other programming languages to more complex math expressions, so I assume that I would be able to in Wolfram too. I'd like to thank the experts on this list, particularly Gianluca Gorni, for providing examples of box manipulation to solve such challenges.
Set Insertion Point: A challenge that I was not able to overcome was that the user has to click inside Feng Shui before typing. I think that the function I need to set the insertion point inside the interface is SelectionMove[], but I was not able to get it to work for me. Any suggestions would be appreciated.
Interface Design: When I first started learning the Wolfram Language, it was easy to make Manipulate[] expressions and deploy them, but it wasn't so obvious how to make and deploy other kinds of user interfaces. Threads on this list indicate that other users have this problem too. Feng Shui and the larger project Chicken Scratch are examples of custom interfaces made with the Wolfram Language.
I've tested the .nb (the code listing below) on Mac OS 10.12.6 using Mathematica 11.0.1.0. I've also attached a .cdf file, which I have tested on Mac and Windows. Enjoy. Let me know if you have any questions.
coverPic =
happySound = Sound[{SoundNote["A5", .02, "Crystal"],SoundNote["C7", .1, "Crystal", SoundVolume -> .75]}];
sadSound = Sound[{SoundNote["AFlat2", .07, "Kalimba", SoundVolume -> .5]}];
font = FontFamily -> "Times New Roman";
magBlue = RGBColor["#000099"];
newQ[] := {
state = 2;
hint = "";
qFormNo = RandomInteger[{1, 4}];
qForm = TraditionalForm[{f[g[x]] == "?", (f\[SmallCircle]g)[x] == "?", g[f[x]] == "?", (g\[SmallCircle]f)[x] == "?"}[[qFormNo]]];
Switch[RandomInteger[{1, 4}],
1, (* f(x)=ax+b g(x)=cx+d *)
diffPts += 50;
co = RandomChoice[DeleteCases[Range[-12, 12], 0], 2];
con = RandomInteger[{-99, 99}, 2];
fx = TraditionalForm[f[x] == co[[1]] x + con[[1]]];
gx = TraditionalForm[g[x] == co[[2]] x + con[[2]]];
If[qFormNo < 3,
ans = Expand[Composition[co[[1]] # + con[[1]] &, co[[2]] # + con[[2]] &][x]];
hintTxt = StringForm["substitute and simplify: `1`", TraditionalForm[co[[1]] (g[x]) + con[[1]]]],
ans = Expand[Composition[co[[2]] # + con[[2]] &, co[[1]] # + con[[1]] &][x]];
hintTxt = StringForm["substitute and simplify: `1`", TraditionalForm[co[[2]] (f[x]) + con[[2]]]]],
2, (* f(x)=ax^2 g(x)=bx *)
diffPts += 125;
co = RandomChoice[DeleteCases[Range[-#, #], 0]] & /@ {3, 12};
con = {};
fx = TraditionalForm[f[x] == co[[1]] x^2];
gx = TraditionalForm[g[x] == co[[2]] x];
If[qFormNo < 3,
ans = Expand[Composition[co[[1]] #^2 &, co[[2]] # &][x]];
hintTxt = StringForm["substitute and simplify: `1`", TraditionalForm[co[[1]] (g[x])^2]],
ans = Expand[Composition[co[[2]] # &, co[[1]] #^2 &][x]];
hintTxt = StringForm["substitute and simplify: `1`", TraditionalForm[co[[2]] (f[x])]]],
3, (* f(x)=ax+b g(x)=cx^2 *)
diffPts += 225;
co = RandomChoice[DeleteCases[Range[-#, #], 0]] & /@ {5, 8};
con = RandomInteger[{-24, 24}];
fx = TraditionalForm[f[x] == co[[1]] x + con];
gx = TraditionalForm[g[x] == co[[2]] x^2];
If[qFormNo < 3,
ans = Expand[Composition[co[[1]] # + con &, co[[2]] #^2 &][x]];
hintTxt = StringForm["substitute and simplify: `1`", TraditionalForm[co[[1]] (g[x]) + con]],
ans = Expand[Composition[co[[2]] #^2 &, co[[1]] # + con &][x]];
hintTxt = StringForm["substitute and simplify: `1`", TraditionalForm[co[[2]] (f[x])^2]]],
4, (* f(x)=ax^2+bx+c g(x)=dx+e *)
diffPts += 325;
co = RandomChoice[DeleteCases[Range[-12, 12], 0], 2];
con = RandomInteger[{-12, 12}];
fx = TraditionalForm[f[x] == x^2 + co[[1]] x + con];
gx = TraditionalForm[g[x] == co[[2]] x];
If[qFormNo < 3,
ans = Expand[Composition[#^2 + co[[1]] # + con &, co[[2]] # &][x]];
hintTxt = StringForm["substitute and simplify: `1`", TraditionalForm[(g[x])^2 + co[[1]] (g[x]) + con]],
ans = Expand[Composition[co[[2]] # &, #^2 + co[[1]] # + con &][x]];
hintTxt = StringForm["substitute and simplify: `1`", TraditionalForm[co[[2]] (f[x])]]]],
diffPts += 43*Count[Flatten[Join[{co}, {con}]], x_ /; x < 0]; (* negatives *)
diffPts += 100*Log10[Total[Abs[CoefficientList[ans, x]]]]; (* ans totals *)
pre = StringForm["`1`\t`2`", fx, gx];
q = qForm;
resp = "";
};
keyDown[k_] := {
If[state != 2, Return];
If[MatchQ[ToCharacterCode[k], ({8} | {127} | {46} | Except[{_?NumberQ}])],
bkSp++;
resp = If[resp === Null || StringLength[resp] < 2, Null, StringDrop[resp, -1]],
If[StringContainsQ["x1234567890^-+", k],
resp = If[resp === Null || resp === "", k, resp <> k];
If[ToExpression[resp] == ans,
EmitSound[happySound];
qCt++;
If[qCt < 6, newQ[], youWon[]]],
EmitSound[sadSound]]];
If[state == 2,
q = StringForm["`1``2`",
qForm /. "?" -> "",
If[resp === Null || resp === "", "?",
char = Characters[resp] /.
"x" -> StyleBox["x", FontSlant -> Italic] //.
{a___, b : Longest[Repeated["1" | "2" | "3" | "4" | "5" | "6" | "7" | "8" | "9" | "0"]], c___} -> {a, StringJoin[b], c} /.
{a___, b_, "^", c_, d___} -> {a, SuperscriptBox[b, c], d} /.
a_ -> RowBox[a];
char // DisplayForm]]]
};
youWon[] := {
state = 3;
bTime = Now;
instructions = "";
elTime = DateDifference[aTime, bTime, "Second"];
timePts = 4000 (120/QuantityMagnitude[elTime])^.6;
accPts = 3000 - 53 bkSp;
score = timePts + accPts + diffPts;
If[score < 6500, score = 6500 - (6500 - score)^.8];
If[score > 9500, score = 9500 + (score - 9500)^.8];
score = Round[score];
pre = "";
q = Style[ToString[score] <> " Points", 72, Blue];
hint = "";
};
showHint := {If[state == 2, bkSp += 9; hint = hintTxt]};
start[] := {
score = 0;
diffPts = 0;
bkSp = 0;
qCt = 0;
aTime = Now;
instructions = Style[StringForm["Complete the function rule.\nType x^2 for `1`.", TraditionalForm[x^2]], 18, font, TextAlignment -> Center];
game = EventHandler[Column[{
Pane[Style[StringForm["`1` to go", Dynamic[6 - qCt]], 20, font], {600, 30}, Alignment -> Right, FrameMargins -> {{0, 8}, {0, 8}}],
Pane[Style[Dynamic[pre], magBlue, 26, font], {600, 50}, FrameMargins -> {{20, 0}, {0, 0}}],
Pane[Style[Dynamic[q], magBlue, 36, font], {600, 160}, Alignment -> Center],
Pane[Style[Dynamic[hint], magBlue, 24, font], {600, 60}, Alignment -> Center],
Row[{
Pane[Button[Style["Start Over", 20, font], newGame[], Appearance -> "Frameless"], {120, 100}, Alignment -> {Left, Bottom}, FrameMargins -> {{8, 0}, {8, 0}}],
Pane[Dynamic[instructions], {360, 100}, Alignment -> {Center, Top}, FrameMargins -> {{0, 0}, {0, 8}}],
Pane[Button[Style["Get Hint", 20, font], showHint[], Appearance -> "Frameless"], {120, 100}, Alignment -> {Right, Bottom}, FrameMargins -> {{0, 8}, {8, 0}}]}]
}, Spacings -> 0], {"KeyDown" :> keyDown[CurrentValue["EventKey"]]}];
newQ[]};
newGame[] := {
state = 1;
game = Button[Image[coverPic, ImageSize -> {600, 400}], start[], Appearance -> "Frameless"];
Framed[Panel[Dynamic[game], Background -> White, FrameMargins -> None], FrameMargins -> None]};
newGame[]
 Attachments:
Attachments: