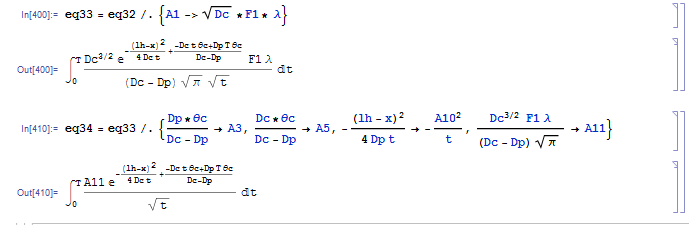Message Boards Message Boards

1
|
4238 Views
|
3 Replies
|
1 Total Likes
View groups...
Share
Share this post:

[?] Use the replace rule correctly?

Jacques Ou
Posted 7 years ago

I used the replace rule, but it didn't work. Would you like to show how to use the replace rule correctly?

In[400]:= eq33 = eq32 /. {A1 -> Sqrt[Dc]*F1* \[Lambda]}

Out[400]= \!\(
\*SubsuperscriptBox[\(\[Integral]\), \(0\), \(T\)]\(
\*FractionBox[\(
\*SuperscriptBox[\(Dc\), \(3/2\)]\ 
\*SuperscriptBox[\(E\), \(\(-
\*FractionBox[
SuperscriptBox[\((lh - x)\), \(2\)], \(4\ Dc\ t\)]\) + 
\*FractionBox[\(\(-Dc\)\ t\ \[Theta]c + Dp\ T\ \[Theta]c\), \(Dc - 
        Dp\)]\)]\ F1\ \[Lambda]\), \(\((Dc - Dp)\)\ 
\*SqrtBox[\(\[Pi]\)]\ 
\*SqrtBox[\(t\)]\)] \[DifferentialD]t\)\)

eq34 = eq33 //. {(Dp*\[Theta]c)/(Dc - Dp) -> A3, (Dc*\[Theta]c)/(
    Dc - Dp) -> A5, -((lh - x)^2/(4 Dp t)) -> -(A10^2/t), (
    Dc^(3/2)  F1 \[Lambda])/((Dc - Dp) Sqrt[\[Pi]] ) -> A11}

Out[409]= \!\(
\*SubsuperscriptBox[\(\[Integral]\), \(0\), \(T\)]\(
\*FractionBox[\(A11\ 
\*SuperscriptBox[\(E\), \(\(-
\*FractionBox[
SuperscriptBox[\((lh - x)\), \(2\)], \(4\ Dc\ t\)]\) + 
\*FractionBox[\(\(-Dc\)\ t\ \[Theta]c + Dp\ T\ \[Theta]c\), \(Dc - 
        Dp\)]\)]\), 
SqrtBox[\(t\)]] \[DifferentialD]t\)\)

enter image description here
POSTED BY: Jacques Ou
3 Replies
Sort By:
Bill Simpson
Bill Simpson
Posted 7 years ago

Please show what eqn30 and eqn31 are so that I can understand what you are trying to do.

Then please try

eq32 = (eq31 /. t -> (T - t))*eq30

eq33 = eq32 /. A1->Sqrt[Dc] F1 \[Lambda]

eqn34 = eqn33 /. (Dp*\[Theta]c)/(Dc-Dp)->A3

eqn35 = eqn34 /. -((lh-x)^2/(4 Dc t)) -> -(A10^2/t)

eqn36 = eqn35 /. (Dc^(3/2)  F1 \[Lambda])/((Dc-Dp) Sqrt[\[Pi]] )->A11

and paste all the results so we can see each substitution separately and try to understand where it is not working
POSTED BY: Bill Simpson
Jacques Ou
Jacques Ou
Posted 7 years ago

I tried in this way. 

eq32 = (eq31 /. {t -> (T - t)})*eq30

(A1 Dc E^(-((lh - x)^2/(4 Dc t)) - t \[Theta]c + (
  Dp (-t + T) \[Theta]c)/(Dc - Dp)))/((Dc - Dp) Sqrt[\[Pi]] Sqrt[t])

eq33 = eq32 /. {A1 -> Sqrt[Dc] F1 \[Lambda]} /. {(Dp*\[Theta]c)/(
      Dc - Dp) -> A3} /. {-((lh - x)^2/(4 Dc t)) -> -(A10^2/t)} /. {(
    Dc^(3/2)  F1 \[Lambda])/((Dc - Dp) Sqrt[\[Pi]] ) -> A11}

(A11 E^(-(A10^2/t) + A3 (-t + T) - t \[Theta]c))/Sqrt[t]

enter image description here

Thanks for your help.

Why the Mathematica codes don't display correctly?
POSTED BY: Jacques Ou
Bill Simpson
Bill Simpson
Posted 7 years ago

Start with

eq1 = (Dc^(3/2) E^(-((lh-x)^2/(4 Dc t))-(-Dc t ?c+Dp T ?c)/(Dc-Dp)) F1 ?)/(Dc-Dp Sqrt[?] Sqrt[t])

Try your substitutions

eq1/.{((Dp ?c)/(Dc-Dp))->A3, (Dc ?c)/(Dc-Dp)->A5, -(lh-x)^2/(4*Dc*t)->-A10^2/t, Dc^(3/2) F1 ?/((Dc-Dp) Sqrt[?])->A11}

Only the A10 substitution succeeds because the other substitutions are within larger expressions.

Use Apart to expose the expressions

Apart[eq1]/.{((Dp ?c)/(Dc-Dp))->A3, (Dc ?c)/(Dc-Dp)->A5, -(lh-x)^2/(4*Dc*t)->-A10^2/t, Dc^(3/2) F1 ?/((Dc-Dp) Sqrt[?])->A11}

Now the A3, A5 and A10 substitutions succeed. But still the A11 substitution does not succeed because it is inside a larger expression.
POSTED BY: Bill Simpson
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract