Introduction
Good day for everyone.
I want to represent one of my work in Wolfram Mathematica. The main idea was a creating of fast algorithm of topology optimization for solid objects. The most commons methods for this is a BESO (Bi-directional evolutionary structural optimization) and SIMP (Solid isotropic material with penalization). Both methods have the same idea: minimization of function like a full-strain energy in object or heat flow through the external surface of object ant etc. Optimization methods have used in aircraft/spacecraft engineering or automobile engineering. So I want to create my own algorithm in Wolfram Mathematica for topology optimization. I wll show some examples with different boundary conditions for proving that this work with different shapes and constraints.
Some examples
Examples of this optimizations:
Minimization of maximum of temperature in radiator: We have metal plate. We must create the shape of this plate which provide us the minimum of maximum temperature in this plate. But we have some constraints: we have a fixed amount of material. We can wisely redistribute all material in space for creating optimal shape. At the beginning of optimization process we have homogeneus structure. Then we apply two algorithms.
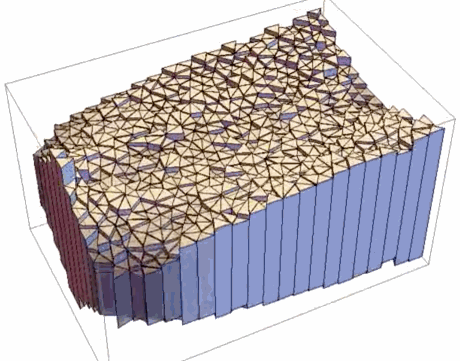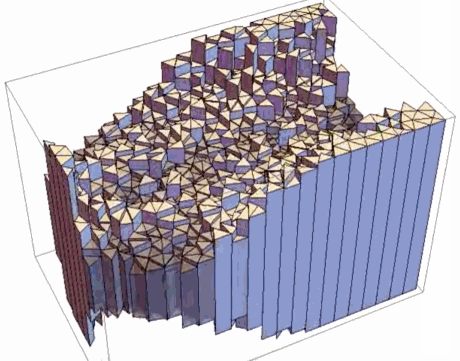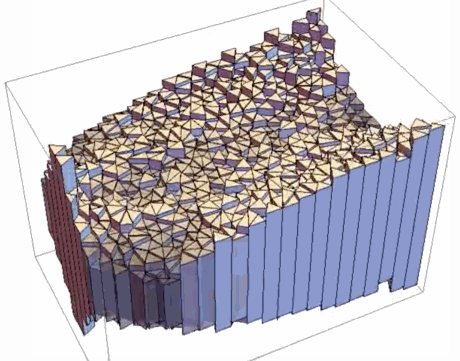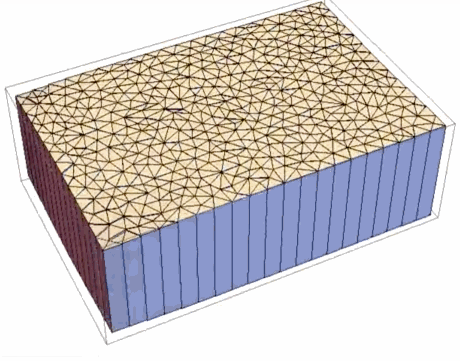
Initial state:
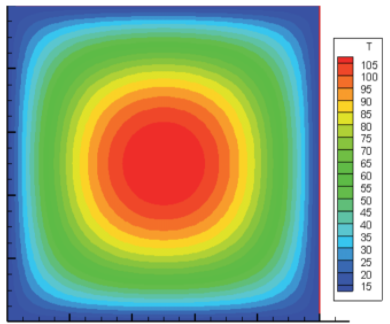
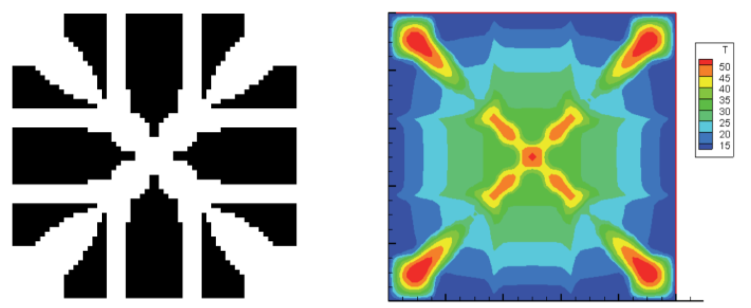
BESO optimization:
SIMP Optimization:
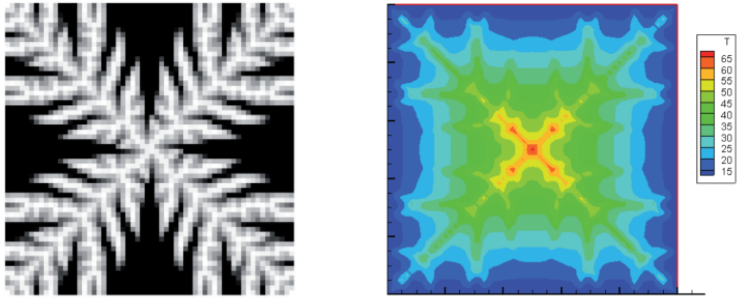
As we see, those algorithms had as results the differents shapes. The main reason is a different types of redistribution of material in space. BESO can only move the mass in space, so we will have the void in space. It marked as black regions on image. In SIMP method we can partially fill the space by material, so we will have gray regions. We can consider many examples of applications both of this methods.
Planning of the work
But I want to show the main Idea of this topic: I wanted to realize SIMP method in Wolfram Mathematica and build my own method for topology optimization. I divided this plan in some steps:
- FEM modelling of 2D objects: plains, shells, beam, etc
- Reproducing the SIMP algorithm in Mathematica over 2D regions
- Checking the results
- FEM modelling of 3D object
- Reproducing the SIMP algorithm over 3D regions
- Checking the results
- Thinking about own idea of topology optimization for minimization of strain energy
- Realization of this idea
- Compairing new method with SIMP
- Optimization of new algorithm
First steps
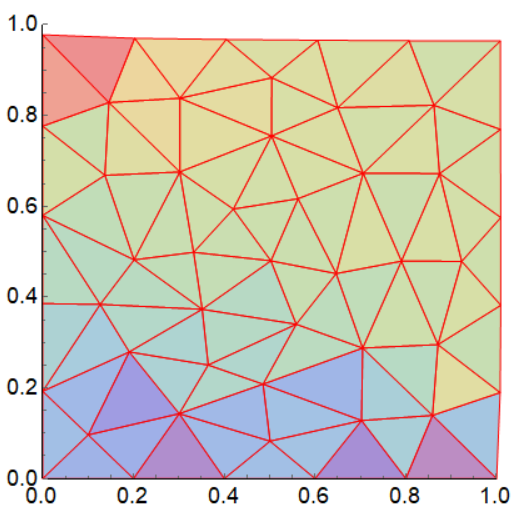
SIMP method based on FEM. It suppose to create virtual field of density. So we have a new parameter for each Finite Element: density. Then we try to find the value of each density which provide us a minimum of goal function. In Wolfram Mathematica we have big diversity of methods for discretization of regions and further analysis. We have a rectangle and discretize it by triangles:
Reg = DiscretizeRegion[Parallelogram[{0, 0}, {{0, a1}, {a2, 0}}], MeshCellLabel -> {0 -> "Index"},
MaxCellMeasure -> .01];
Coord = MeshCoordinates[Reg];
Polys = MeshCells[Reg, 2];
ActionSquare = Show[Reg, ImageSize -> 600]

Polys contains all information about each Finite Element (Triangles), Coord contains all coordinates of all points. By this data we can construct the Stiffness Matrix of this object for solving the Stress-Strain problem. As the result of solving this problem we get the vectors of displacements, strains and stresses in each finite element. We can visualize it, as examples: von Mises stresses in axis-Symmetrical problem, red - biggest stresses, blue and violet - lowest stresses:
2D Solutions of SIMP method
Then we can use SIMP method algorithm on this solution for redistributing the material in space, we move the material from non-stressed areas into area with big amount of stresses. SIMP - iterative method, so we will get a result after some steps. SIMP also have a big amount of control parameters: penalizing factor, continuum coefficient and etc.
- Big size of cells:
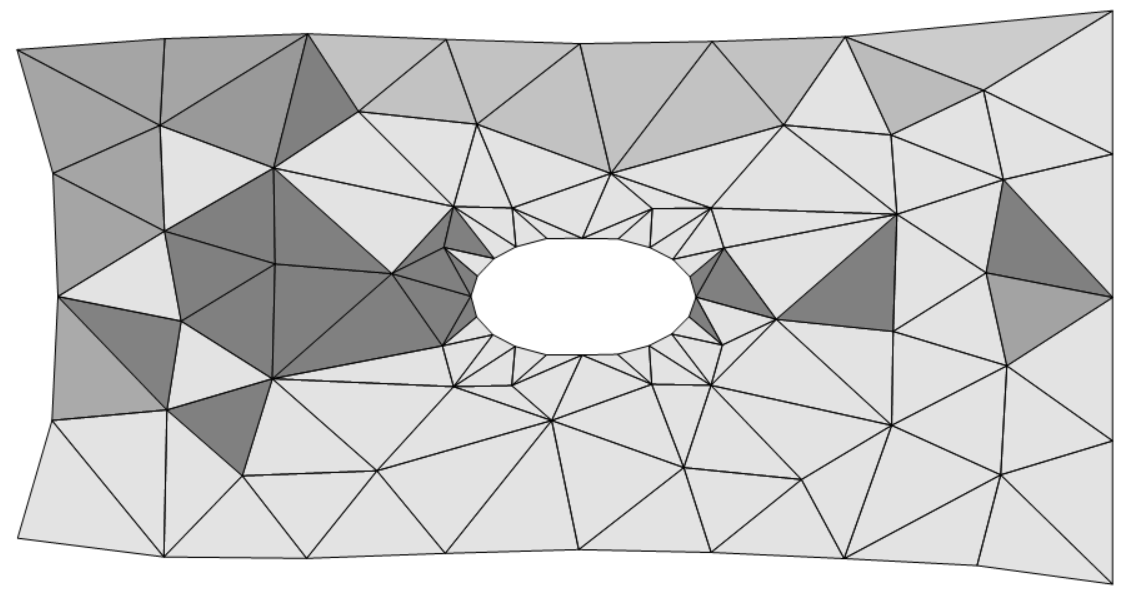
- Small cells:
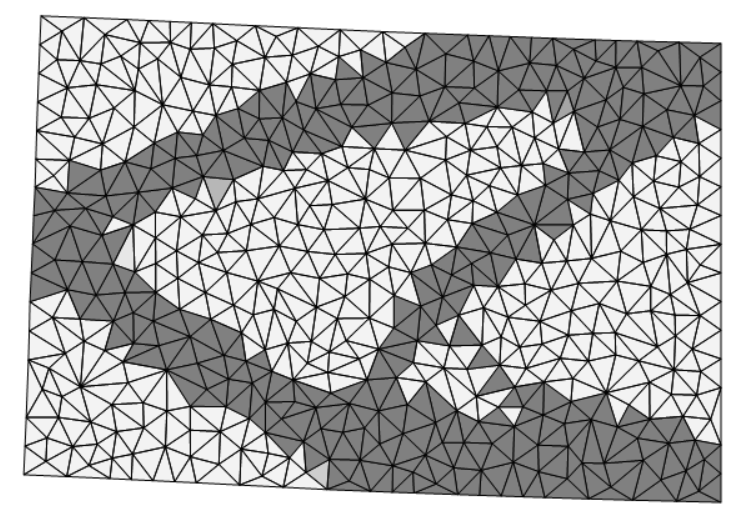
We can analyse the main criteria of optimization: full energy of strain
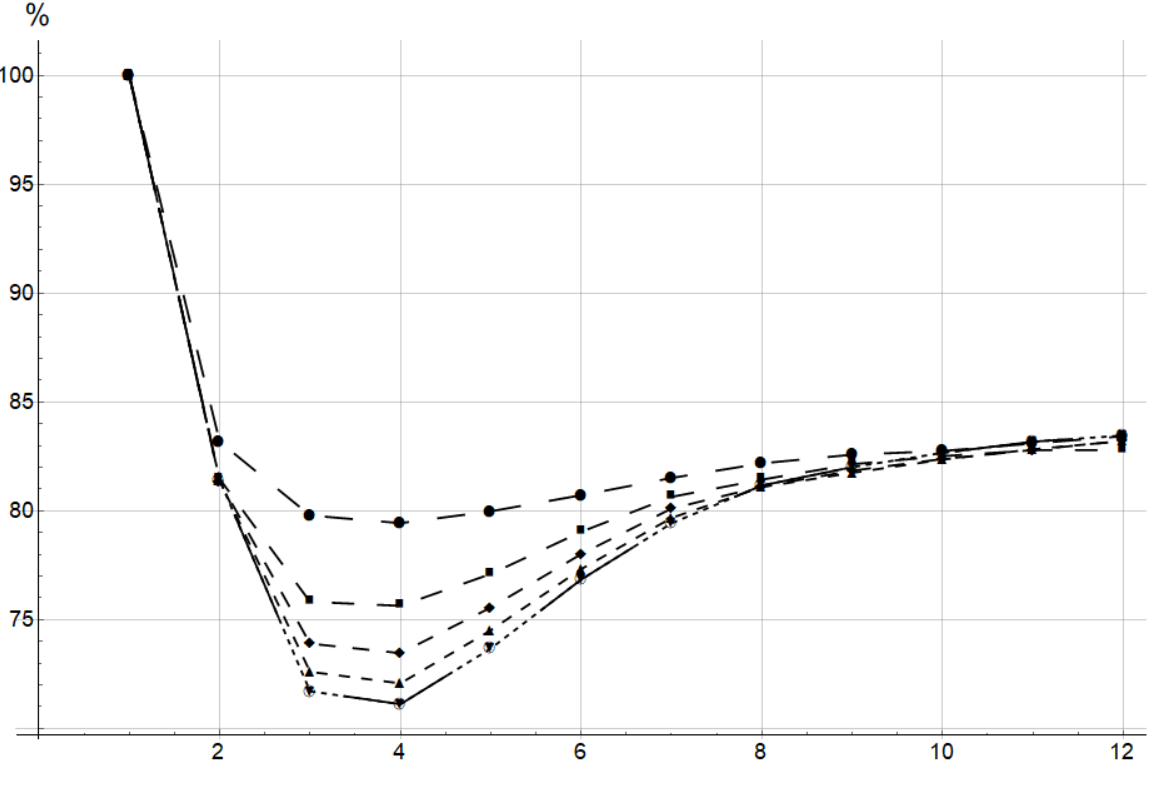
X-axis is an iteration of SIMP method, so we get final solution at 12~13 step. Different dashing - different parameters of optimization, we see that it change only the "way" of optimization. We can see that energy decreases from step to step, so the main goal was completed. So I realized the SIMP method in WM. You can look at this on my GitHub.
Main Part
We must do the same things in 3D. I will skip all explanations in this part because they are the same as in 2D. I will show some examples of optimization:
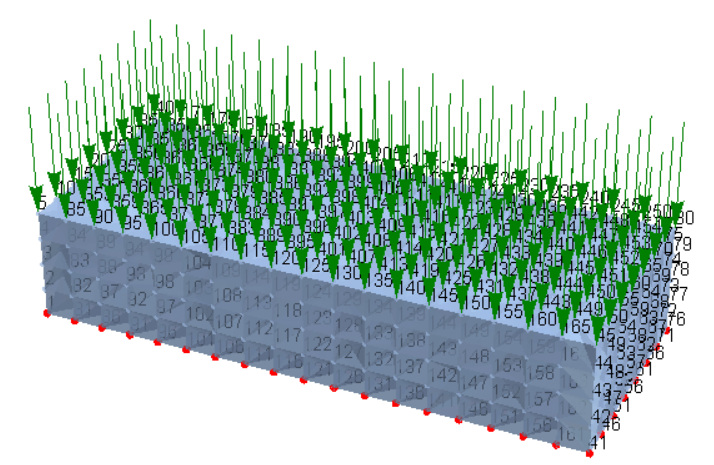
- Result of SIMP Optimization
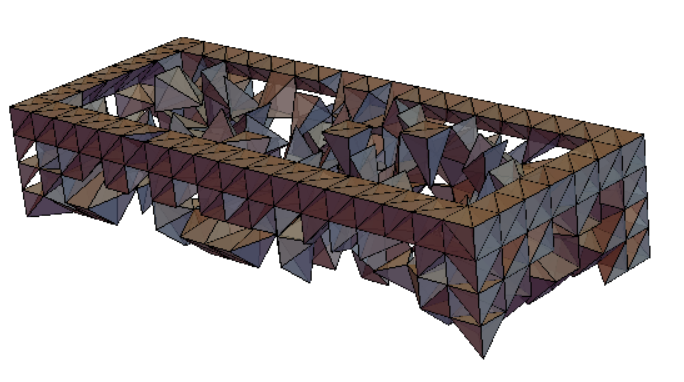
But I must say that in case of 3D problem the level of computations grows very fast. So on my notebook it is very hard to analyse the big amount of Finite Elements for Topology optimization. I began to seek the to minimize my computations. We have only a hypothesis about existing only one global extremum point of our function. If we consider that it is true we have a very fast solution. We must construct a goal function of many arguments.
goalFunction = displacement.StifnessMatrix.displacement;
massEquation =
Sum[V[[k]]*density[[k]], {k, 1, Length[Tetras]}] ==
Sum[V[[k]], {k, 1, Length[Tetras]}]*0.75;
densityEq = Thread[0.0 <= # <= 1 &[density]];
The goal function is a strain energy in solid object. Arguments - densities of Finite Elements. And also we have some constraints, we can't involve new mass in space, our elements can't be overcrowded. displacement it is a vector of displacements of each points of our discretized object. We get it from solving Stress-Strain problem. StiffnessMatrix we get from the properties of our object. density is vector of density of each finite element.
sysOfEq = Flatten[{goalFunction, massEquation, Equation, densityEq}];
variables = Flatten[{density, DisplacementI}];
Here we construct the system of equation for our problem and vector of our variables. I suppose to use FindMinimum function for finding the global minimum of our function. But we must define the initial point for seeking the minimum point.
initDis = Thread[{#, 0} &[DisplacementI]];
initDen = Thread[{#, 0.5} &[density]];
initCond = Flatten[{initDen, initDis}, 1];
Then we try to run the FindMinimum with this initial conditions and equations:
resultFMin =
Quiet[FindMinimum[sysOfEq, initCond,
Method -> "InteriorPoint"]]; // AbsoluteTiming
And after this, I got the incredible results. The vectors of density for SIMP method and FindMinimum ?oincide almost completely. I got the increasing of computation speed near x40 in compairing with SIMP algorithm. You can look at all result also on my GitHub.
Conclusions
- FindMinimum give the same result as the SIMP method for stress-strain problem;
- It has a very big advantage in time in compairing with SIMP, SIMP/FindMinimumTime~40-50;
- I must prove the hypothesis about the one global minimum of the multidimensional function. If anyone can give me some advices about this.
- We can use this for constructing optimized models for 3D printing. It was introduced in WM v11.0.0
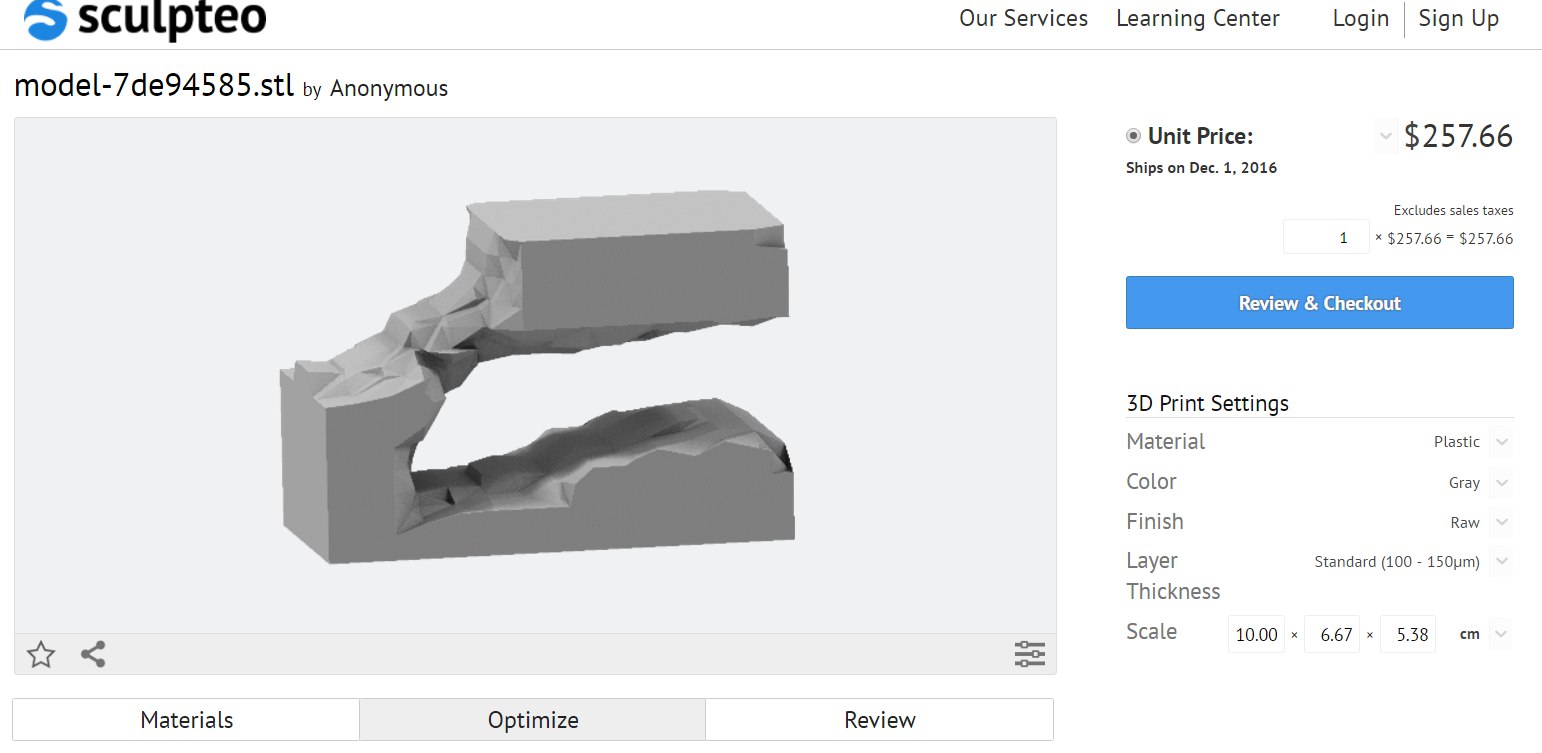
Further explorations
- In Mathematica we can find some FEM packages: NDSolve
FEM or ACEFEM package from Korelc Joe. I want to try connect them in something.
- Create the CDF application for simpliest application of Topology Optimization.
- Further analysis of finding the global minimum of goal function.
- Improving the algorithm of constructing StiffnessMatrix and finding minimum. I mean construct own specialized function for this problem.
Questions
- How I can prove the existing only one minimum of multidimensional function with Mathematica.
Link for video
Video