Dear Wolfram Community,
For my work I am using a mechanical system and have to find the relation between a linear displacement x and a certain angle alpha. To find x as a function of alpha is fairly easy and results in the following function:
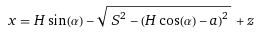
Where H = 80mm, S = 205mm, a = 68mm, and z = 204.5mm are all system parameters. x is the linear displacement and alpha is the input angle.
I also need the inverse of this function (alpha = f(x)), but had troubles deriving this function by hand. Hence, I tried to have Wolfram Alpha find the inverse for me. This results in quite an extensive formula, which I'm ok with:
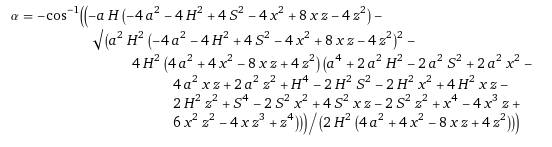
However, if I supply this function with a certain linear displacement, I do not get the expected (right?) answer. E.g. with an alpha of 40 degrees or 0.698 radians I get a linear displacement of 51mm (using the first equation), which seems to be correct. However, using 51mm as input for alpha = f(x) gives -3.018.
What am I doing wrong?
Thank you for your help. Matthijs