Interesting problem. I've never used FindPeaks before and thought that you just could feed it with any arbitrary 2D set of points and get back directly the 2D coordinates of the peak.
The problem seems to be that FindPeaks can only deal with regularly sampled data.
1. Values Method
That is why, one possible input for FindPeaks is simply a sequence of 1D values (with their positions playing the role of abscissa). In your example, you correctly give as input only the sequence of the ordinates and get the relative positions of the peaks:
peaks = FindPeaks[fakedata[[All, 2]]]
{{4, 133}, {13, 133}, {39/2, 127}}
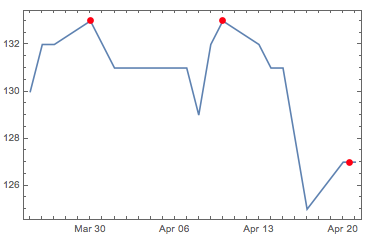
Two peaks (with value 133) are detected in the 4th and 13th positions of the sequence corresponding respectively to the dates {2015,3,30} and {2015,4,10}. The last peak (value 127) is most interesting as it is located at position 39/2=19.5, between position 19 and 20 of your input list : in the fakedata list that would correspond to the 20th of April 2015 at noon !
Then, the main problem is how to convert back these positions (4,13,39/2) into their real abscissas (which in addition here are time entities !). The solution was already given above (by Sander Huisman), and consists in directly interpolating the abscissas.
ip = Interpolation[AbsoluteTime /@ fakedata[[All, 1]], InterpolationOrder -> 1];
By default, the interpolation order is 3, so it is better to make it explicitly linear here.
You can for example then check that 39/2 corresponds indeed to the 20th of April at noon:
ip[39/2] // DateObject

Then:
ipeaks = MapAt[ip, peaks, {All, 1}];
DateListPlot[fakedata, Epilog -> {Red, PointSize[0.02], Point[ipeaks]}]
2. TimeSeries method
The documentation says also that FindPeaks can input regularly sampled time series, which is not the case with your data
RegularlySampledQ@fakedata
False
but we can convert and resample:
fakedataseries =
TimeSeries[fakedata] //
TimeSeriesResample[#, Join[#["Dates"][[{1, -1}]], {"Day"}],
ResamplingMethod -> {"Interpolation", InterpolationOrder -> 1}] &;
You now have a regularly sampled time series which you can directly (2D coordinates) feed in FindPeaks and get the final peaks:
RegularlySampledQ@fakedataseries
True
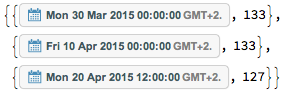
speaks = FindPeaks[fakedataseries]["DatePath"]
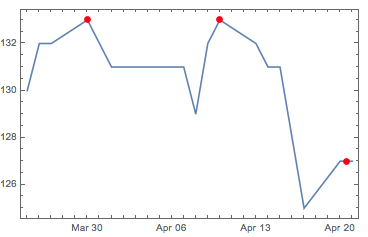
DateListPlot[fakedata, Epilog -> {Red, PointSize[0.02], Point[speaks]}]
3. PeakDetect
Finally, you can have a look at the function PeakDetect which seems to work almost as FindPeaks but does not interpolate the positions of the peaks and makes it possible to retrieve directly all of them:
dpeaks = Pick[fakedata, PeakDetect[fakedata[[All, 2]]], 1];
DateListPlot[fakedata, Epilog -> {Red, PointSize[0.02], Point[dpeaks]}]
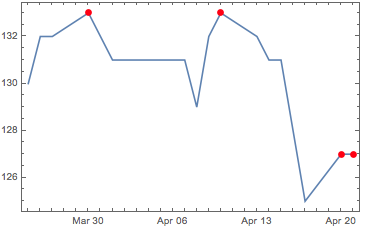
However, note now the last two peaks instead of one interpolated peak with FindPeaks.
Anyway, it would be nice if FindPeaks could take care of these problems directly, maybe in some future version.