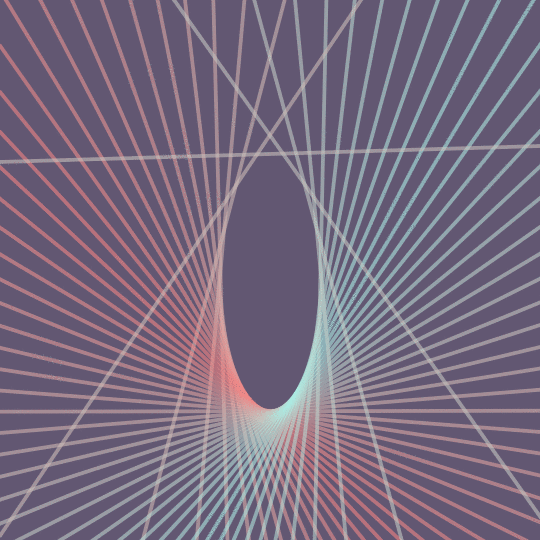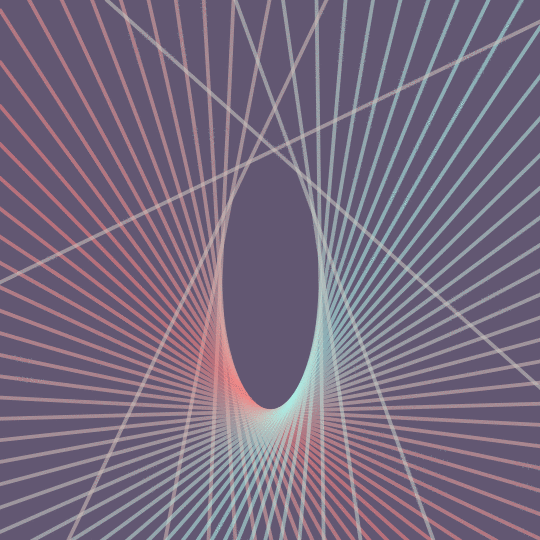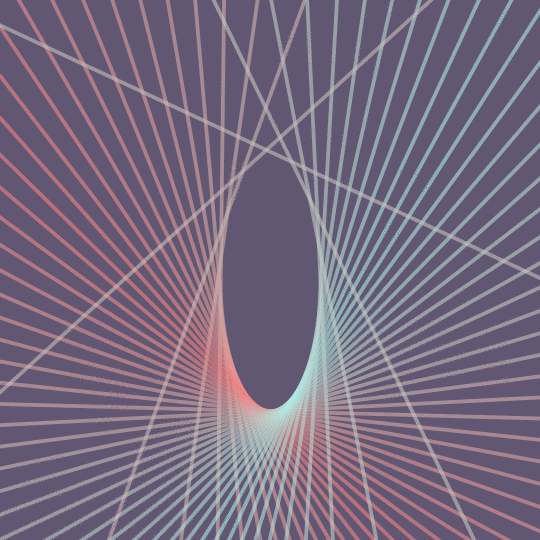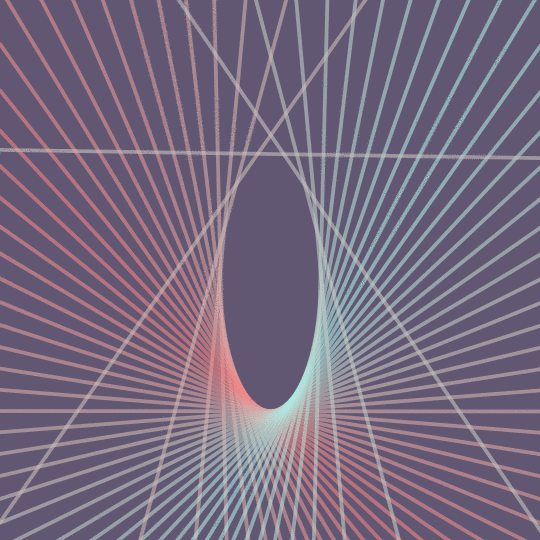
Thread the Needle
Returning to some ideas I've discussed before (see Light Show, Stay Upright, and Horizon), we can think of the real projective plane $\mathbb{RP}^2$ as parametrizing the space of lines in the plane.
More precisely, recall that $\mathbb{RP}^2$ is the space of all lines in $\mathbb{R}^3$ that pass through the origin (or, if you like, the 1-dimensional linear subspaces of $\mathbb{R}^3$). Of course, any line through the origin in 3-space has a unique perpendicular 2-plane that passes through the origin: its orthogonal complement. This tells you that $\mathbb{RP}^2$ is the same thing as the Grassmannian $G_2(\mathbb{R}^3)$, which is the space of all 2-dimensional planes through the origin in $\mathbb{R}^3$.
Now, to get lines in the plane, think of the plane as the $z=1$ plane in $\mathbb{R}^3$. Then (almost) every plane through the origin intersects the $z=1$ plane in a line, and conversely every line in the $z=1$ plane lies in a unique plane through the origin. Therefore, the Grassmannian $G_2(\mathbb{R}^3)$, which is also just the projective plane $\mathbb{RP}^2$, parametrizes lines in the plane. (The parenthetical caveat is that the $z=0$ plane passes through the origin and does not intersect the $z=1$ plane at all; this is the so-called "line at infinity", and if we're being careful we would say that the Grassmannian is really parametrizing lines in the projective plane.)
Any point on the sphere can be thought of as a unit vector, which determines a unique line through the origin, and hence, by the above construction, a line in the plane. Here it is in code:
SpherePointToLine[p_] := Block[{b, pts},
b = NullSpace[{p}];
pts = #[[;; 2]]/#[[3]] & /@ b;
InfiniteLine[pts]
]
Now, to make the animation I'm just taking some evenly-spaced points on a circle on the sphere, rotating them around the circle, and then translating into lines in the plane. The circle is given by rotating the point Normalize[{1, 1, 1.11}] around the axis $(0, 1, 1.6)$. Here's the code:
With[{n = 50, cols = RGBColor /@ {"#F38181", "#A9EEE6", "#625772"}},
Manipulate[
Graphics[
{Thickness[.007], Opacity[.6],
Table[
{Blend[Append[cols[[;; -2]], cols[[1]]], Mod[(? + t)/(2 ?), 1]],
SpherePointToLine[
RotationMatrix[t + ?, Normalize[{0, 1, 1.6}]].Normalize[{1, 1, 1.11}]]},
{?, -?/2, 2 ? - ?/2 - 2 ?/n,
2 ?/n}]},
PlotRange -> {{-20, 20}, {-10, 30}}, Background -> cols[[-1]],
ImageSize -> 540],
{t, 0., 2 ?/n}]
]