Dear Raivat Shah,
are you looking for a solution over the Reals or Integers? I guess that it is a good idea to start with the equalities such as:
FindInstance[(10!)/(10^n)*(1/(10 - n)!) == 0.5 && n > 0, n, Reals]
{{n -> 4.01848}}
or else
FindInstance[(10!)/(10^n)*(1/(10 - n)!) == 0.5 && n > 0, n, Integers]
{}
You might want to look at:
Plot[{(10!)/(10^n)*(1/(10 - n)!), 0.5}, {n, 0, 20}, PlotRange -> All]
and
Plot[{(10!)/(10^n)*(1/(10 - n)!), 0.5}, {n, 0, 80}, PlotRange -> All]
Also look at this
Table[(10!)/(10^n)*(1/(10 - n)!), {n, 1, 1000}]
and this (you might want to play with the PlotPoints option)
LogPlot[Abs@{(10!)/(10^n)*(1/(10 - n)!), 1/2}, {n, 0, 60}, PlotRange -> All, PlotPoints -> 10000]
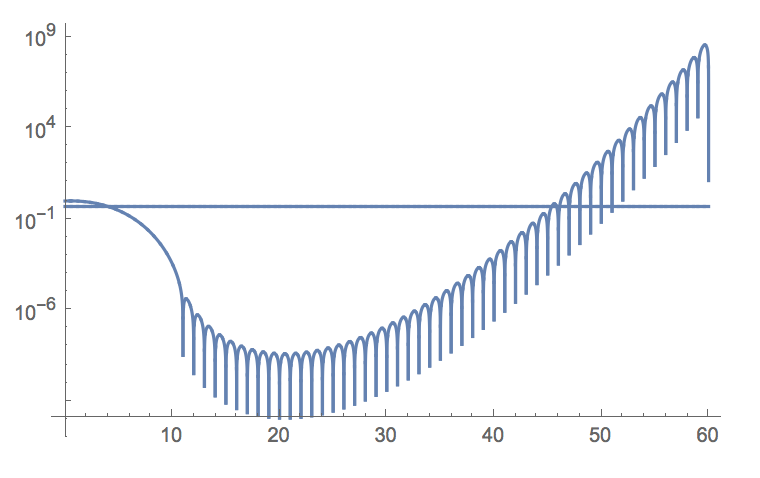
Can you guess what is going on? Once you see that, it might help you to solve the original inequality.
Best wishes,
Marco
PS: This here might also be useful:
Plot[n!, {n, -10, 0}]