Another reason is that they use different algorithms and sometimes domains (Complexes, Reals).
For a Plot-like solver for the real roots of a smooth function over an interval, consider this:
{x -> #} & /@ Reap[
NDSolve[{y'[x] == f, y[a] == (f /. x -> a),
WhenEvent[f == 0, Sow[x, "root"]]}, {}, {x, a, b}],
"root"
][[2, 1]]
WhenEvent uses FindRoot under the hood. Of course it might well miss double roots, just like Plot, that NSolve might actually catch.
Example:
NSolve[Re@PolyLog[2, x] - Sin[x] + x/10 == 0 && 1 < x < 100, x]
(*
NSolve::nsmet: This system cannot be solved with the methods available to NSolve.
NSolve[x/10 + Re[PolyLog[2, x]] - Sin[x] == 0 && 1 < x < 100, x]
*)
ClearAll[nsolve]; (* general solver based on the above idea *)
nsolve[eq_, {x_, a_, b_}] := Module[{y},
With[{f = eq /. Equal -> Subtract},
{x -> #} & /@ Reap[
NDSolve[{y'[x] == f, y[a] == (f /. x -> a),
WhenEvent[f == 0, Sow[x, "root"]]}, {}, {x, a, b}],
"root"
][[2, 1]]
]];
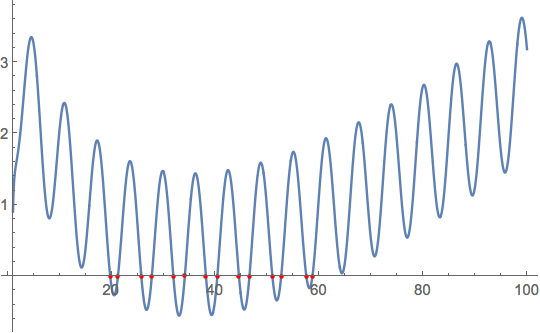
roots = nsolve[Re@PolyLog[2, x] - Sin[x] + x/10 == 0, {x, 1, 100}]
(*
{{x -> 19.7212}, {x -> 21.2187}, {x -> 25.7155}, {x -> 27.743}, {x ->
31.8867}, {x -> 34.0993}, {x -> 38.1639}, {x -> 40.3583}, {x ->
44.523}, {x -> 46.5435}, {x -> 50.9595}, {x -> 52.6584}, {x ->
57.4995}, {x -> 58.675}}
*)
Plot[Re@PolyLog[2, x] - Sin[x] + x/10, {x, 1, 100},
Mesh -> {x /. roots}, MeshStyle -> Red]