i trying to define a function that depend of IC within a coupled of PDEs system. The system is show below:

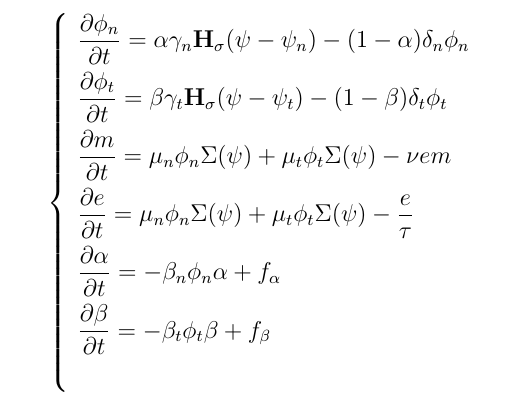
The function is $\Sigma(\psi)$ where $\psi = \phi_n + \phi _t + m$ and the ICs are precisely $\phi _n = 0.45 $, $\phi _t = 0.005 $ , $m = 0.45 $ but i don't have idea to define $\Sigma$ function in my code.

My code is below

H[s_, \[sigma]_] := Which[s <= 0, 1, s > \[sigma], 0, True, 1 - s/\[sigma]]

solucion[t_] = 
 With[{gaman = 0.746, gamat = 0.97, psi0 = 0.75, psin = 0.6, psit = 0.8, deltat = 0.03, deltan = 0.1, mun = 0.1, 
 mut = 0.05, nu = 0.000016, pin = 6000000, pit = 3000000, \[Tau] = 0.005, fo = 0.25, fg = 0.16, betan = 1.3, 
 betat = 1.2, Kan = 0.1, Kat = 0.3, \[Kappa] = 0.00000734, D = 1.0},

NDSolve[{
 fin'[t] == oxi[t]*gaman*fin[t]*H[s, \[sigma]] (psi - psin) - ((1 - alpha[t]))*deltan*fin[t],

 fit'[t] == glu[t]*gamat*fit[t]*H[s, \[sigma]] (psi - psit) - ((1 - beta[t]))*deltat*fit[t],

 m'[t] == mun*fin[t] + mun*fit[t] - nu*e[t]*m[t],

 e'[t] == pin*fin[t] + pit*fit[t] - e'[t]/\tau,

 alpha'[t] == -betan*fin[t]*alpha[t] + fo,

 beta'[t] == -betat*fit[t]*beta[t] + fg,

 fin[0] == 0.45, fit[0] == 0.005, m0] == 0.2, e[0] == 0.2, 
 alpha[0] == 0.25, beta[0] == 0.16}, {fin[t], fit[t], m[t], e[t],
 alpha[t], beta[t]}, {t, 0, 80}] /. {s -> 0, \[sigma] -> 1}][[1, All, 2]]

 Plot[solucion[t], {t, 0, 80}, PlotRange -> {{0, 80}, {0, .55}}]

In my code above i haven't included the $\Sigma(\psi)$ nor defined $\psi = \phi_n + \phi _t + m$. The Sigma function appears in eqs 3 and 4 [m y e], in the code are m'[t] and e'[t]

Is it possible? Could you please help me?

Any suggestions are very appreciated. Thanks