I am confused by this prospect. We have a semicircle with radius r whose centroid is given by 4r/3pi. Can we obtain the area of the semi circle by integrating from the centroid of the semi circle.
I saw that we could integrate from the centre of the full circle by evaluating integral through a sector like this 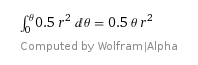
But how could we do it from the centroid of the semi circle?