Set Up Functions Describing Ellipse and Cassini Oval
rule to translate and rotate coordinates
rottransrl[{xc_, yc_, \[Theta]_}, {x_, y_}] =
Thread[{x, y} -> RotationMatrix[-\[Theta]].{x - xc, y - yc}];
function describing an ellipse with axes {a,b}, center {xc,yc} and orientation [Theta]
ell[{a_, b_}, {xc_, yc_, \[Theta]_}] = (x/a)^2 + (y/b)^2 - 1 /.
rottransrl[{xc, yc, \[Theta]}, {x, y}];
function describing a Cassini oval with axes {a,b}, center {xc,yc} and orientation [Theta]
oval[{a_, b_}, {xc_, yc_, \[Theta]_}] = ((x - a)^2 + y^2) ((x + a)^2 + y^2) -
b^4 /. rottransrl[{xc, yc, \[Theta]}, {x, y}];
Generate Regions for Elllipse and Cassini Oval
ellipse region with axes {a,b}, center {xc,yc} and orientation [Theta]
el = ImplicitRegion[ell[{a, b}, {xc, yc, \[Theta]}] <= 0, {x, y}];
Cassini oval region with axes {1,5/4}, centered at {1/7,0} and rotated by [Pi]/10
ov = ImplicitRegion[oval[{1, 5/4}, {1/7, 0, \[Pi]/10}] <= 0, {x, y}];
Attempt to find smallest area ellipse with oval contained in it, Using RegionWithin and NMinimze
TimeConstrained[
sln = NMinimize[{a*b, RegionWithin[el, ov], a >= 0, b >= 0}, {a, b, xc,
yc, \[Theta]}, Method -> {"NelderMead", "PostProcess" -> False}], 360]
$Aborted
Reformulate Problem Using Lagrange Multipliers
function to generate Lagrange multiplier equations for finding extreme values for function describing curve1 for points on curve2.
curveWithinLagMults[curve1_, curve2_, vars_List] :=
Join[Thread[D[curve1 == \[Lambda]*curve2, {vars}]], {curve2 == 0,
curve1 == r}]
use NSolve to find the solutions to the Lagrange multiplier equations
curveWithinNSolve[curve1_, curve2_, vars_List] :=
NSolve[curveWithinLagMults[curve1, curve2, vars], Join[vars, {\[Lambda], r}],
Reals]
function to find the maximum value of ellipse function for points on the Cassini oval
f[a_?NumericQ, b_?NumericQ, xc_?NumericQ, yc_?NumericQ, \[Theta]_?NumericQ] :=
Max[r /. curveWithinNSolve[ell[{a, b}, {xc, yc, \[Theta]}],
oval[{1, 5/4}, {1/7, 0, \[Pi]/10}], {x, y}]]
find the minimum area ellipse containing the Cassini oval
AbsoluteTiming[
sln = NMinimize[{a*b, f[a, b, xc, yc, \[Theta]] <= 0, a >= 0, b >= 0}, {a, b,
xc, yc, \[Theta]}, Method -> {"NelderMead", "PostProcess" -> False}]]
NMinimize::incst: NMinimize was unable to generate any initial points satisfying the inequality constraints {f[a,b,xc,yc,[Theta]]<=0}. The initial region specified may not contain any feasible points. Changing the initial region or specifying explicit initial points may provide a better solution.
NMinimize::nosat: Obtained solution does not satisfy the following constraints within Tolerance -> 0.001`: {f[a,b,xc,yc,[Theta]]<=0}.
{95.9544, {1.61441, {a -> 1.62478, b -> 0.993618, xc -> 0.145382,
yc -> -0.000172813, \[Theta] -> 0.305791}}}
plot the result
p = ContourPlot[{oval[{1, 5/4}, {1/7, 0, \[Pi]/10}] ==
0, (ell[{a, b}, {xc, yc, \[Theta]}] /. sln[[2]]) == 0}, {x, -2,
2}, {y, -2, 2}, ImageSize -> Small];
find the extremum points
pts = curveWithinNSolve[(ell[{a, b}, {xc, yc, \[Theta]}] /. sln[[2]]),
oval[{1, 5/4}, {1/7, 0, \[Pi]/10}], {x, y}]
{{x -> -1.34479, y -> 0.0336357, \[Lambda] -> 0.155498,
r -> -0.0117827}, {x -> 1.63088, y -> -0.0328177, \[Lambda] -> 0.154844,
r -> -0.0186086}, {x -> -0.0933478, y -> 0.711853, \[Lambda] -> 0.324496,
r -> -0.428871}, {x -> 1.6821, y -> 0.433738, \[Lambda] -> 0.121384,
r -> -0.0326298}, {x -> -1.39363, y -> -0.445365, \[Lambda] -> 0.121615,
r -> -0.0267585}, {x -> 0.38161, y -> -0.711032, \[Lambda] -> 0.323676,
r -> -0.431725}, {x -> -1.01925, y -> -0.913277, \[Lambda] -> 0.161002,
r -> 0.00116534}, {x -> 1.29604, y -> 0.91782, \[Lambda] -> 0.162165,
r -> -0.00179309}}
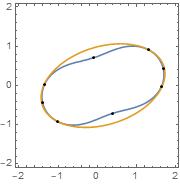
show the result with the extremum points
Show[p, Graphics @ Point[{x, y} /. pts]]