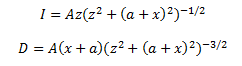Hi
I am not a Mathematica user, I am just looking for a math package that can solve my problem.
I need to solve a system of two rather complicated power equations, like those in the image below. Here x and z are the unknown variables, all other constants are known. Can Mathematica do that?
But actually I need even more. I will have a set of values for the known constants I and D (A and a are fixed). So I will need not just one solution but a set of solutions for each pair of (I, D). So, if I feed the set of (I,D) pairs into Mathematica, can it produce a set of solutions for me, not just one solution?