I am modeling sperm/egg diffusion and want to manipulate the variable "d" with respect to the integral shown below in my code. However, in order to make my results meaningful, for each value of d, I need to solve for each time "t" when the inner integrand = 0 (once again refer to the equation below). This is because of the fact that the probability < 0 after a certain value of "t" and I only want to add up positive values/probabilities. The following is an example of a Probability of Mating Versus Time Graph I made at d = 2: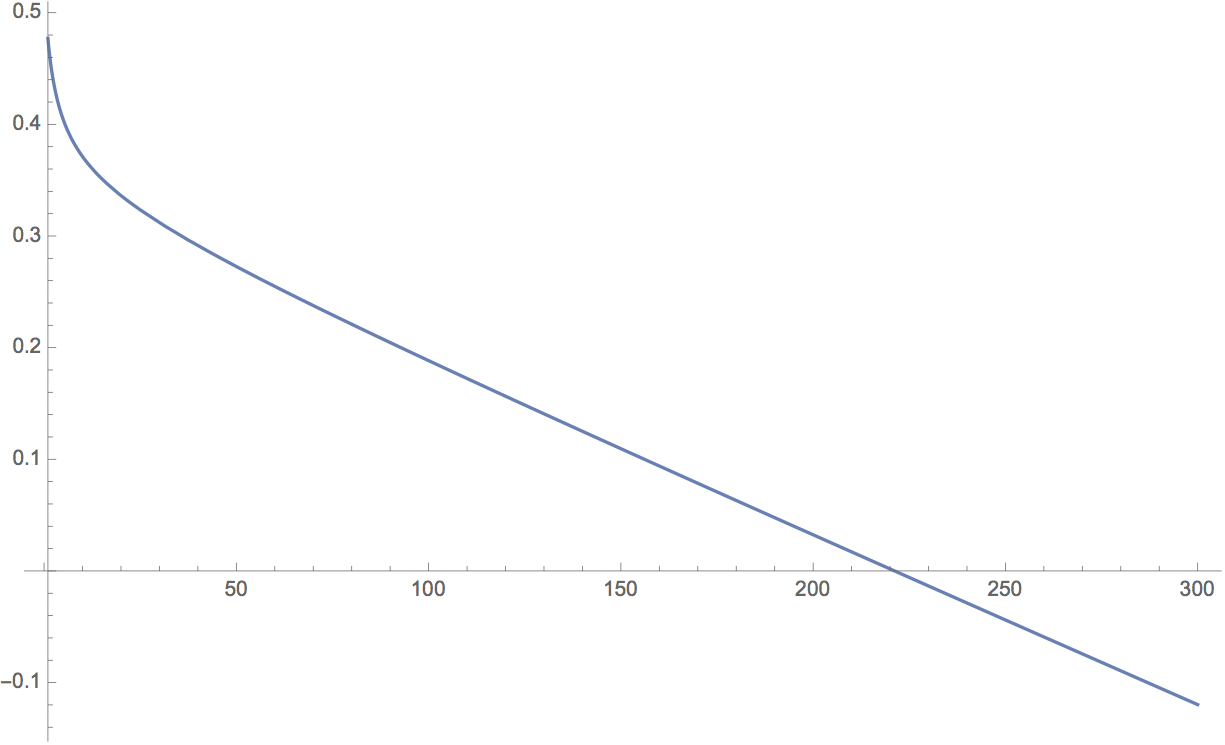

As you can see, after approximately t = 220, the values become negative. So, I want to integrate this graph (and be able to manipulate this process for all other graphs at variant d-values) from {1, the EXACT time where probability = 0}. In the example above, the boundaries are approximately when t goes from {1, 220}. The problem is that, for every value of d, the time "t" where probability = 0 CHANGES, hence why I am asking this question.

Here is my code:

s[x_, y_, t_] = 1/Sqrt[4*Pi*t]*E^((-(x + 0)^2 - (y + 0)^2)/(4*t));

e[x_, y_, t_, d_] = 1/Sqrt[4*Pi*t]*E^((-(x + d)^2 - (y + d)^2)/(4*t));

f2D[sc_, t_] = N[(171.153*sc - 0.149*t + 31.334)/100];

N[Integrate[N[(N[Integrate[If[s[x, y, t] > 0 && e[x, y, t, d] > 0, (e[x, y, t, d] + s[x, y, t])*f2D[s[x, y, t], t], 0], {x, -\[Infinity], \[Infinity]}, {y, -\[Infinity], \[Infinity]}]])/(2*N[Integrate[1, {x, -\[Infinity], \[Infinity]}, {y, -\[Infinity], \
\[Infinity]}, {z, 0, s[x, y, t]}]])], {t, 1, 220}]]

I have tried to add as the boundary at the end (last line of code)

{t, 1, Solve[(e[x, y, t, d] + s[x, y, t])*f2D[s[x, y, t], t] == 0, t, Reals}

but this seems to not work even before beginning to manipulate the d-values because the result of the solving is an equation instead of a number (you need context, meaning it needs to solve for when the actual integrand = 0 if that makes sense). Henceforth, I surmise that the solving process for these "t" upper bounds must either be incorporated into the integrating process (during the process) or possibly before the integration process and systematically substitute each value into the upper bound of the process. The latter appears to be more time consuming and all efforts to emulate its procedure have failed.

With all of that being said, how do I make this process of finding each specific t-value (as an upper bound) for every d-value work properly? Can I afterward tack on

Manipulate[...]

or

Plot[...]

and be able to manipulate the entire process with respect to the changing d-values?

Any assistance would be very much appreciated! This is my first discussion, so please take it easy on me in terms of formatting and structure :)