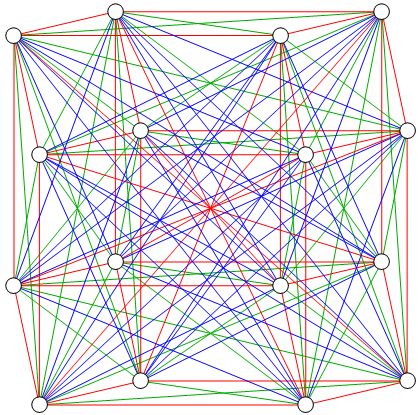
Some of the points in a unit distance Tesseract graph are at a distance of $\sqrt3$, which allows a pair of equilateral triangles between them.
tesser ={RootReduce[CirclePoints[8]/(EuclideanDistance@@CirclePoints[8][[{1,2}]])],RootReduce[RotateRight[CirclePoints[8],4]/(EuclideanDistance@@CirclePoints[8][[{1,4}]])]};
extra=Flatten[Table[RootReduce[
{a,b}/.Solve[{EuclideanDistance[tesser[[1,k]],{a,b}]==1,EuclideanDistance[tesser[[2,Mod[k+c,8,1]]],{a,b}]==1}]],{k,1,8}, {c,-1,1,2}],2];
tesserlines=
Sort/@Select[Subsets[Flatten[tesser,1],{2}], Chop[Quiet@N[1-EuclideanDistance@@#]]==0&];
otherlines= Complement[Sort/@Select[Subsets[Join[extra,Flatten[tesser,1]],{2}], Chop[Quiet@N[1-EuclideanDistance@@#]]==0&],tesserlines];
splitlines=Complement[Sort/@Select[Subsets[#,{2}], Chop[Quiet@N[1-EuclideanDistance@@#]]==0&],tesserlines]&/@ConnectedComponents[Graph[#[[1]]<->#[[2]]&/@otherlines]];
Graphics[{Darker[Green],Line/@tesserlines,Red,Line/@splitlines[[1]],Blue, Line/@splitlines[[2]],EdgeForm[Black],White,Disk[#,.03]&/@Join[extra,Flatten[tesser,1]]}]
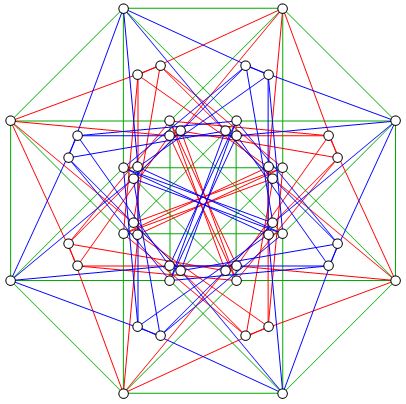
This reminded me of a way to split the 24-cell into three tesseract graphs.
v24cell=Join[Flatten[tesser,1],{{-10,0},{0,-10},{0,10},{10,0},{-4 Sqrt[2],-4 Sqrt[2]},{-4 Sqrt[2],4 Sqrt[2]},{4 Sqrt[2],-4 Sqrt[2]},{4 Sqrt[2],4 Sqrt[2]}}/9];
e24cell={{{15,12},{9,14},{12,9},{11,16},{14,11},{13,10},{16,13},{15,10},{5,10},{5,4},{15,4},{9,6},{7,6},{7,12},{11,8},{1,8},{1,14},{13,2},{3,2},{3,16},{16,5},{5,6},{6,11},{8,13},{7,8},{10,7},{2,15},{1,2},{12,1},{4,9},{3,4},{14,3}},{{22,10},{12,22},{18,10},{18,12},{20,14},{20,12},{14,21},{21,12},{19,16},{19,14},{16,23},{23,14},{17,10},{17,16},{10,24},{24,16},{22,6},{6,19},{19,4},{4,22},{6,21},{8,17},{21,8},{17,6},{8,23},{2,18},{23,2},{18,8},{2,24},{4,20},{24,4},{20,2}},{{18,13},{18,15},{24,15},{13,24},{20,9},{20,15},{15,22},{22,9},{19,11},{19,9},{9,21},{21,11},{17,13},{17,11},{11,23},{23,13},{5,24},{3,19},{19,5},{24,3},{7,22},{5,17},{22,5},{17,7},{1,21},{7,18},{21,7},{18,1},{3,23},{1,20},{23,1},{20,3}}};
Graphics[{Darker[Green],Line[v24cell[[#]]]&/@e24cell[[1]],Red,Line[v24cell[[#]]]&/@e24cell[[2]],Blue, Line[v24cell[[#]]]&/@e24cell[[3]],EdgeForm[Black],White,Disk[#,.03]&/@Flatten[cell24,2]}]
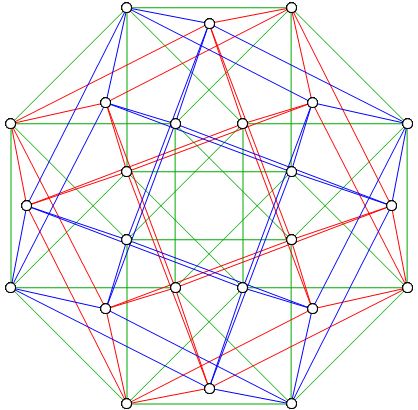
Add diagonals to a tesseract graph and you get the Clebsch graph. So I was reminded of the way to split $K_{16}$ into three Clebsch graphs.
clebsch ={
{{12,11},{12,16},{12,13},{12,5},{12,7},{3,14},{3,6},{3,4},{3,16},{3,7},{8,4},{8,9},{8,11},{8,1},{8,7},{2,6},{2,15},{2,13},{2,1},{2,7},{14,10},{14,11},{14,13},{14,1},{6,9},{6,11},{6,5},{4,15},{4,13},{4,5},{10,15},{10,9},{10,5},{10,7},{15,11},{15,16},{9,16},{9,13},{16,1},{1,5}},
{{12,3},{12,14},{12,4},{12,10},{12,15},{3,8},{3,11},{3,1},{3,5},{8,2},{8,6},{8,15},{8,16},{2,4},{2,10},{2,9},{2,5},{14,6},{14,9},{14,16},{14,5},{6,4},{6,13},{6,1},{4,11},{4,7},{10,16},{10,13},{10,1},{15,9},{15,13},{15,7},{9,11},{9,1},{11,16},{11,13},{16,7},{13,5},{1,7},{5,7}},
{{12,8},{12,2},{12,6},{12,9},{12,1},{3,2},{3,10},{3,15},{3,9},{3,13},{8,14},{8,10},{8,13},{8,5},{2,14},{2,11},{2,16},{14,4},{14,15},{14,7},{6,10},{6,15},{6,16},{6,7},{4,10},{4,9},{4,16},{4,1},{10,11},{15,1},{15,5},{9,5},{9,7},{11,1},{11,5},{11,7},{16,13},{16,5},{13,1},{13,7}}};
HeilbronnCoordinates = {{0, 31/33}, {8/31, 1}, {1, 23/33}, {23/31, 7/11}, {2/31, 7/11},
{10/31, 23/33}, {29/31, 1}, {21/31, 31/33}, {10/31, 2/33}, {2/31, 0},
{21/31, 10/33}, {29/31, 4/11}, {8/31, 4/11}, {0, 10/33}, {23/31, 0}, {1, 2/33}};
Graphics[{Darker[Green],Line[HeilbronnCoordinates[[#]]]&/@clebsch[[2]],Red,Line[HeilbronnCoordinates[[#]]]&/@clebsch[[1]],Blue, Line[HeilbronnCoordinates[[#]]]&/@clebsch[[3]],EdgeForm[Black],White,Disk[#,.03]&/@HeilbronnCoordinates}]