Thank you for helping me with case #1. Do you reckon it is a bug or I
am missing some important distinction between a and {a} in this
context?
You should avoid using {a} in this context, since this is supposed to output a list containing the value of the PDF at a, rather than just outputting the value at a. But there does seem to be a bug; when I evaluate
PDF[TransformedDistribution[x + x, x \[Distributed] DiscreteUniformDistribution[{1, 6}]], {3}]
the output is {1/6}, rather than {0}, which is what it should be. And indeed
PDF[TransformedDistribution[x + x, x \[Distributed] DiscreteUniformDistribution[{1, 6}]], 3]
correctly evaluates to 0.
In general, it seems like there's something screwy about the internal representation of PDFs of discrete distributions. For example,
PDF[DiscreteUniformDistribution[{1, 6}]]
should be a pure function which evaluates to
$1/6$ on the integers 1, 2, 3, 4, 5, 6 and to 0 on everything else, but instead it is
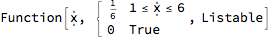
which will happily evaluate to
$1/6$ when you plug in
$1.1$ (or, presumably, any other real number between 1 and 6), but PDF[DiscreteUniformDistribution[{1, 6}], 1.1] correctly evaluates to 0.
As for your second issue, I have no idea what the problem is. There's obviously some difference between the Mathematica back end and the Wolfram Programming Lab back end, but again the issue seems to be with discrete distributions. Replacing DiscreteUniformDistribution[{1,6}] with UniformDistribution[{1,6}] in your code produces entirely reasonable output even in Wolfram Programming Lab. So it may well be the case that both of your issues have the same root cause, whatever it is.
Conclusion: there are bugs in the Mathematica/Wolfram implementation of (PDFs of) discrete probability distributions.