This is the pelican which Neural Networks(VGG-16) look.

I referred this post to the presentation by Markus van Almsick at the 2017 Wolfram Technology Conference. In addition to the information posted here, this presentation contains a variety of interesting and useful information of how to use WL deep learning framework.

Introduction VGG-16

VGG-16 is one of the representative models in deep learning to identify the main object in an image. Fortunately we can get the pre-trained VGG-16 from the Wolfram Neural Net Repository.

vgg16 = NetModel["VGG-16 Trained on ImageNet Competition Data"]

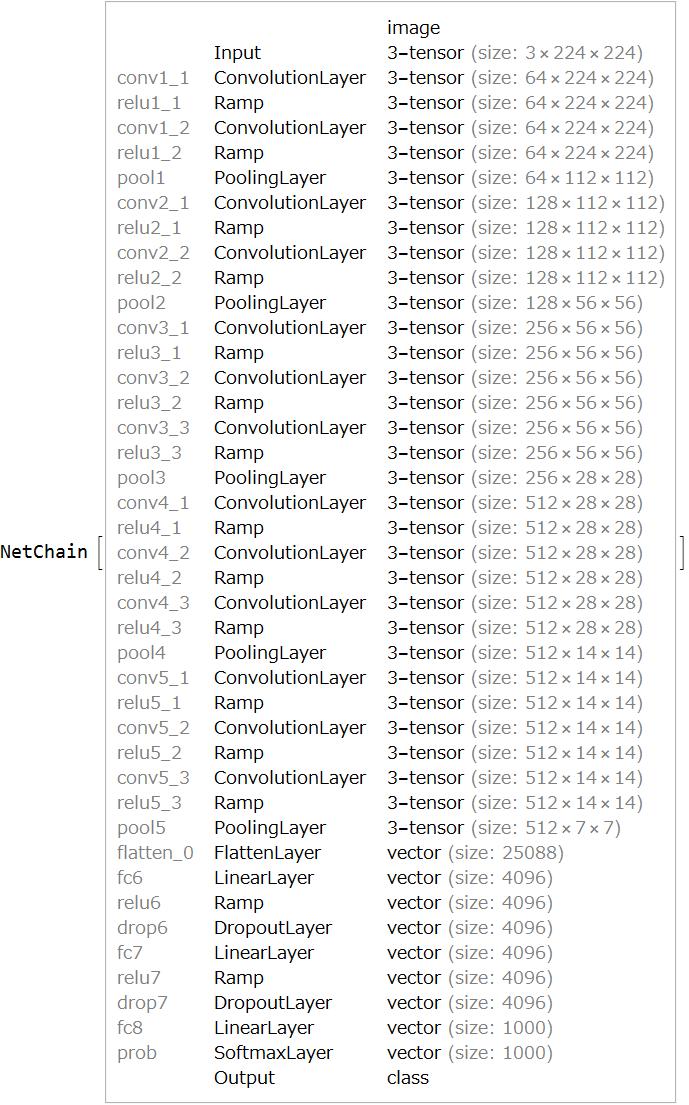
VGG-16 is able to identify an image.

The probability is 99.59%

vgg16[img, {"TopProbabilities", 1}]

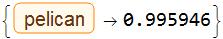
What is the pelican of the probability 1(=100%) ?

What does VGG-16 look?

Find an image to maximize the part(145th element) corresponding to the pelicans of the output(size:1000 vector) of the layer fc8 which is the layer before the last of VGG-16.

NetExtract[vgg16, "fc8"]

classes = NetExtract[vgg16, "Output"];
pelican = 
 Position[Normal[classes]["Labels"], 
   Entity["Concept", "Pelican::jpfg7"]][[1, 1]]

145

Start with an image of all 0, then gradually tweak the image towards what VGG-16 looks like pelican. Define a loss function below as each element of the output is 0 or more and NetTrain minimizes the loss.

Loss = NetChain[{ElementwiseLayer[x \[Function] -x]}];

Create a new network using the subnet of VGG-16.

net = NetGraph[<|
   "image" -> 
    ConstantArrayLayer["Array" -> ConstantArray[0., {3, 224, 224}]], 
   "vgg16subnet" -> Take[vgg16, {1, -2}],
   "select" -> PartLayer[pelican],
   "Loss" -> Loss |>,
  {"image" -> "vgg16subnet" -> "select" -> "Loss", 
   "Loss" -> NetPort["Loss"] }]

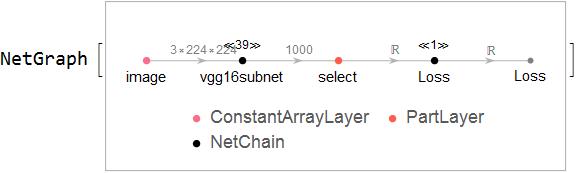
Train the new network. The training data is dummy as it is unnecessary. And the subnet of VGG-16 does not undergo training and is left unchanged by NetTrain.

Off[First::nofirst]
trainedNet = NetTrain[net, <|0 -> {0}|>, "Loss",
   LearningRateMultipliers -> {"image" -> 1, _ -> None},
   MaxTrainingRounds -> 2000];

Retrieve the image that VGG-16 looks like pelican from the trainedNet.

meanColor = Normal[NetExtract[vgg16, "Input"]]["MeanImage"];
idec = NetDecoder[{"Image", "MeanImage" -> meanColor}];
vgg16pelican = 
 idec[NetExtract[NetExtract[trainedNet, "image"], "Array"]]

vgg16[vgg16pelican]

The probability of this image is 100%!

vgg16[vgg16pelican, {"TopProbabilities", 1}]

Examples

What does each layer of the VGG-16 look?

As the same above, find an image to maximize the activation of the filters in different convolutionLayers of the VGG-16.

There are 13 ConvolutionLayers.

layernames = (NetExtract[vgg16, All] // Keys);
convlist = Select[layernames, StringTake[#, 1] == "c" &]

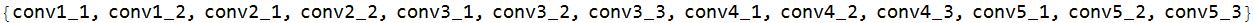
The number of filters in each convolutionLayer is

(NetExtract[NetExtract[vgg16, #], "Output"] & /@ convlist)[[All, 1]]

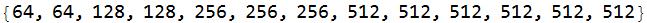
Start with an image of all 0, then gradually tweak the image to maximize the activation of each filter. Define a loss function below.

Loss = NetChain[{ElementwiseLayer[x \[Function] x^2], 
    SummationLayer[], ElementwiseLayer[x \[Function] -x]}];

Create new networks and train the networks of the first 10 filters in each layer.

Off[First::nofirst]
result = {};
Do[
 subnet = Take[vgg16, {1, convlist[[j]]}];
 Do[
  net = NetGraph[<|
     "image" -> 
      ConstantArrayLayer["Array" -> ConstantArray[0., {3, 224, 224}]], 
     "vgg16subnet" -> subnet,
     "select" -> PartLayer[i],
     "Loss" -> Loss |>,
    {"image" -> "vgg16subnet" -> "select" -> "Loss", 
     "Loss" -> NetPort["Loss"] }];
  trainedNet = NetTrain[net, <|0 -> {0}|>, "Loss",
    LearningRateMultipliers -> {"image" -> 1, _ -> None},
    MaxTrainingRounds -> 300, BatchSize -> 1];
  AppendTo[result, 
   idec[NetExtract[NetExtract[trainedNet, "image"], "Array"]]];,
  {i, 10}];,
 {j, Length[convlist]}]

Retrieve the image that each filter looks from the trainedNet. These images gradually become more complex patterns as the layer becomes deeper.

Grid[Join[{Join[{""}, Range[10]]}, 
  Flatten[{convlist[[#]], Partition[result, 10][[#]]}] & /@ 
   Range[Length[convlist]]], Frame -> All, Spacings -> {.5, .5}]