Message Boards Message Boards

Interest rates derivatives in multi-curves framework

Igor Hlivka, MThree Consulting
Posted 7 years ago

We discuss the changes to the interest rates processes when we move from mono-curve setting to multi-curve framework. This is characterised by presence of several curves – a dedicated discount curve and set of estimation curves – each for specific Libor rate. The first is generally assumed to be the OIS curve, whilst the rest are ‘tenor’ curves for given Libor tenor.

The changes in the forward Libor estimation are due to the ‘loss’ of martingale property when mono-curve world is replaced by multiple curve framework. We show how multiplicative adjustment works in this new setting and how interest rate derivatives are affected. Various modelling assumptions are used to show derivatives pricing in this new setting.

enter image description here

Introduction

We review the setting of Interest rate derivatives in post-crisis era characterised by multi-curve environment where dedicated yield curves are defined for forward rate estimation and cashflow discounting. The multi-curve framework is a direct consequence of financial crisis of 2007-2008 when the so-called 'Libor market' - represented by single yield curve stopped being seen as risk-free, and new curves started to emerge to better reflect the counterparty risk in the financial markets.

The current interest rate framework exists in the simplest form in the dual curve setting - (i) discounting curve - usually built with OIS instruments and (ii) estimation curve - generally used to build the 'main' estimation curve in a given currency. This is 3 month Libor curve for USD or 6 months Euribor curve for EUR.

Existence of dual curve environment does change the interest rate mathematics. Martingales defined in the single curve framework do not hold and the process has to be adapted to account for curves duality. We demonstrate how this process work and show how interest rate derivatives - both linear and optional work when we move from the singe to dual framework.

Interest rate derivatives in a single curve framework

We firs look at the single-curve homework in the pre-2007 era. When only one yield curve exists, the derivatives pricing is simple and tidy. Forward rate defined on the singe curve using two deposits coincides the forward rate agreement rate = FRA rate

Subscript[F, S] = 1/(Subscript[T, 2] - Subscript[T, 1]) * P[0, Subscript[T, 1]]/P[0, Subscript[T, 2]] - 1;

where Subscript[F, S] is the forward rate in a single-curve setting, Subscript[T, 1], Subscript[T, 2] and tow maturity dates with Subscript[T, 2]>Subscript[T, 1] and P[0, Subscript[T, 1]] , P[0,Subscript[T, 2]] are two discount factors at time 0 with maturities Subscript[T, 1] and Subscript[T, 2]. The FRA rate is then defined as Subscript[F, FRA] = K such that the payoff of the contract at time 0 has value = 0 L[Subscript[T, 1], Subscript[T, 2]] - K = 0 with L[Subscript[T, 1], Subscript[T, 2]] defined as forward term-rate.

Interest rate swaps in single-curve setting

Interest rate swap together with FRA are one the simplest linear interest rate derivatives. It usually involves exchange of fixed rate for a series of floating forward rates up to final maturity:

fixedLeg = S Sum[\[Delta][i] P[0, i], {i, 1, m}]
floatLeg = Sum[\[Delta][i] P[0, i] Subscript[L, S][i], {i, 1, n}]

enter image description here

where $L_S$ is the forward Libor rate in a single curve framework. This is identical to the FRA rate defined above:

Subscript[L, S][i] = 1/\[Delta][i]*(P[i - 1]/P[i]-1)

floatLeg = 
 Sum[\[Delta][i]* 
   P[0, i]*(1/\[Delta][i])*(P[0, i - 1]/P[0, i] - 1), {i, 1, n}]

P[0, 0] - P[0, n]

Then swap rate S is simply a solution to the equation:

Solve[fixedLeg == floatLeg, S]

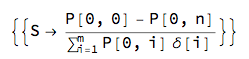
enter image description here

This shows that in a single-curve framework the swap rate is simply a difference in two discount factors normalised by $annuity= \sum_{i = 1}^n\delta[i]\ P[0, i]$. The same curve is used to produce discount factors that are used for (i) discounting and (ii) forward Libor estimation.

Multi-curve framework for Interest rate derivatives

When we move to multi-curve setting, we assume:

  • Separate discounting curve - generally OIS curve
  • Separate estimation curve for 'main index - 3M or 6M
  • Separate estimation curves for 'minor indices - say 1M, 12M or 6M (in 3M setting)

When the discounting curve is set to the OIS curve, we define the OIS forward rate with tenor h similarly to the forward in the mono-currency setting: 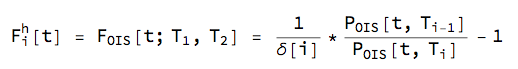enter image description here

for i = 1...n where $\delta[i]$ is a year fraction for interval $T_{i-1} -T_i$ and $P_{OIS}[t,T_i]$ is a discount factor from the OIS curve at time t maturing at time $T_i$

In the multi-curve framework, the Libor definition in the single curve environment does not hold L[Subscript[T, 1],Subscript[T, 2]]] != Subscript[F, S][t;Subscript[T, 1],Subscript[T, 2]] != Subscript[F, OIS][t,Subscript[T, 1],Subscript[T, 2]] since the discount factors in definition of Libor when only one curve is used is not the same as in dual curve case. Libor is dual curve setting is calculated from the estimation curve with unique set of discount factors.

The expectation of forward Libor in the dual curve setting can be expressed as \!( *SubsuperscriptBox[(E), (t), SubsuperscriptBox[(Q), (OIS), (T2)]]([))Subscript[F, D][Subscript[T, 1];Subscript[T, 1],Subscript[T, 2]]] = Subsuperscript[E, t, Subsuperscript[Q, OIS, T2]][E^Subsuperscript[Q, OIS, T2][L[Subscript[T, 1],Subscript[T, 2]|Subscript[[ScriptCapitalF], t]]. The valuation of forward rate agreement with Libor forward rate is therefore defined as: FRA[t,Subscript[T, 1],Subscript[T, 2]] =Subscript[P, OIS][t,Subscript[T, 2]] [Delta][Subscript[T, 1],Subscript[T, 2]] \!( *SubsuperscriptBox[(E), (t), SubscriptBox[(Q), (OIS)]]([))L[t,Subscript[T, 1],Subscript[T, 2]]-K].

Current market practice takes a shortcut and simply values the FRA as FRA[t,Subscript[T, 1],Subscript[T, 2]] =Subscript[P, OIS][t,Subscript[T, 2]] [Delta][Subscript[T, 1],Subscript[T, 2]] (L[t,Subscript[T, 1],Subscript[T, 2]]-K]) where discount factor Subscript[P, OIS][t,Subscript[T, 2]] comes from the OIS curve and the forward Libor L[t,Subscript[T, 1],Subscript[T, 2]] is taken from the estimation curve. This is clearly inconsistent since forward Libor is NOT martingale under the OIS forward measure.

Libor adjustment in multi-curve framework

To restore the non-arbitrage relationship, forward Libor rate has to be adjusted. We refer to this as Forward basis that restores the equilibrium between Subscript[F, OIS] and Subscript[F, E]. Assuming multiplicative basis Aj, we get:

Fd = (1/\[Delta]) (Pd[T1]/Pd[T2] - 1);
Fe = (1/\[Gamma]) (Pe[T1]/Pe[T2] - 1);
Solve[Fe \[Gamma] == Fd \[Delta] Aj, Aj]

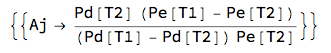
enter image description here

where Subscript[F, d] represents forward rate from the OIS curve, Subscript[F, e] is the forward Libor from the estimation curve, Subscript[P, d] is a discount factor f from the OIS curve and Subscript[P, e] is a discount factor from the estimation curve.

The forward basis is therefore a ratio of discount factors from both curves and can be recovered ex-post once both curve have been calibrated to the market data.

From modelling perspective, however it is desirable to express the forward rate in terms of single curve. We introduce new discount factor adjustment Subscript[B, j] and re-calculate the forward adjustment spread:

Fd = (1/\[Delta]) (PdT1/PdT2 - 1);
Fe = (1/\[Gamma]) (PeT1/PeT2 - 1);
PeT1 = BjT1 PdT1;
PeT2 = BjT2 PdT2;
Solve[Fd == Fe Aj, Aj] // Simplify

enter image description here

and get the forward Libor $F_e$

Fe

enter image description here

This shows that the Libor is a function of (i) OIS curve and (ii) discount factor adjuster. To proceed, we assume that the forward rate follows LogNormal martingale dynamics under forward measure Subscript[Q, e]

Fe = GeometricBrownianMotionProcess[0, \[Sigma], x0];
Fe[t]

![enter image description here][8]

We apply to similar process to the forward adjuster defined under forward measure $Q_d$

Bj = GeometricBrownianMotionProcess[0, \[Eta], y0];
Bj[t]

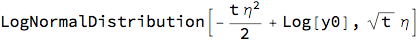
enter image description here

To change the measure from Subscript[Q, e]==> Subscript[Q, d], we use the change-of-measure technique that says:
Subscript[E, OIS][Fe] = Subscript[E, e][Fd Bj]. To change the measure, we need joint expectation of OIS forward and the forward adjuster. We apply the Binormal Copula with LogNormal marginals

cDist = CopulaDistribution[{"Binormal", ?}, {Fe[t], Bj[t]}];
cdrift = Expectation[x*y, {x, y} \[Distributed] cDist, 
  Assumptions -> 
   t > 0 && ? > 0 && ? > 0 && -1 <= ? <= 1]

enter image description here

The joint expectation of forward OIS and forward adjuster on relative basis provides the adjustment for the process where the change of measure occurs. Since the martingale process for forward Libor has to be drift less, we adjust the forward rate by its negative quantity;

Aj = cdrift/(x0 y0) /. t -> -t

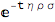
enter image description here

Returning back to our original Libor adjustment formula, we observe: 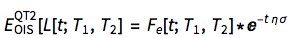enter image description here

Fe_Adj = Expectation[x, x \[Distributed] Fe[t], 
    Assumptions -> t > 0 && ? > 0 && x0 > 0]*Aj /. x0 -> L[0]

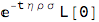
enter image description here

This is the forward Libor rate under the OIS forward discounting measure. The adjustment is a function (i) time, (ii) volatility of Libor and (iii) volatility of OIS rate. A reader familiar with the exposition above, an recognise here the parallelism to process drift adjustment in the foreign currency market know as 'quanto adjustment'. The similarity is obvious - we work with two curves, two sources and randomness and switch the measure similarly to what we do in foreign currency markets.

Forward rate agreement - FRA

This is the simple contract that pays the difference between forward Libor and fixed rate 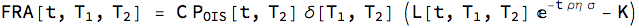enter image description here

where [DoubleStruckCapitalC] is nominal and $\delta[\tau]$ is a year fraction on day count convention between the Libor tenor $T_1$ and $T_2$.

Ho much does the adjustment affects the FRA valuation? We look first at market volatilities - (i) for the Libor rate and (ii) Adjuster:

Assume: $\delta=0.25$, C=1 mil, $P_{OIS}[t,T_2] = 0.98$, t=1, L=0.0125,K=0.0125

fra = C*Pois*?*(L*E^(-t*?*?*?) - K) /. {C -> 
    1000000, L -> 0.0125, K -> 0.0125, t -> 1, ? -> 0.25, 
   Pois -> 0.98, ? -> 0.75}
Plot3D[fra, {?, 0.1, 0.3}, {?, 0.1, 0.3}, 
 AxesLabel -> Automatic, PlotTheme -> "Marketing", 
 PlotLabel -> 
  Style["FRA valuation impact by market volatilities", Blue, 15]]

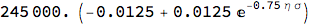
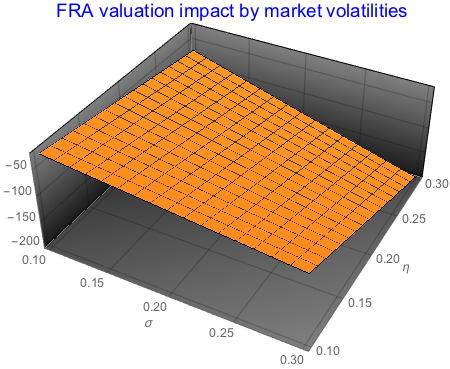
enter image description here

enter image description here

As we can see from the graph above, higher volatilities will push the value of forward rate lower and therefore making the value of long forward contract more negative. The opposite applies to a short FRA contract.

We can now look at correlation impact:

fra2 = C*Pois*?*(L*E^(-t*?*?*?) - K) /. {C -> 
     1000000, L -> 0.0125, K -> 0.0125, t -> 1, ? -> 0.25, 
    Pois -> 0.98, ? -> 0.2, ? -> 0.2};
Plot[fra2, {?, -0.75, 0.75}, PlotStyle -> Red, 
 PlotLabel -> Style["Correlation impact on FRA valuation", Blue, 15]]

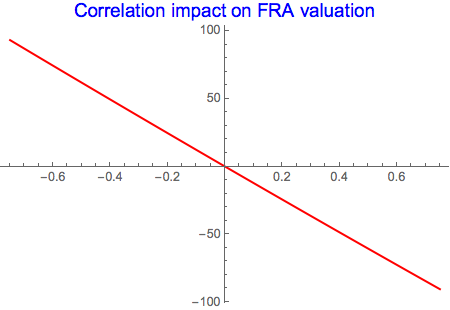
enter image description here

Negative correlation will increase the long FRA value since the adjusted Libor will be higher. Positive correlation will drive the valuation i into negative territory.

Interest rate swap - IRS

The payer IRS formula is determined from the same equation: fixed leg = float leg

fixedLeg = K Sum[?[i] Subscript[P, OIS][i], {i, 1, m}];
floatLeg = 
  Sum[?[i] Subscript[P, OIS][i] L[
     i] Exp[-Subscript[t, i] ? ? ?], {i, 1, n}];
swapR = Solve[fixedLeg == floatLeg, K] // Simplify

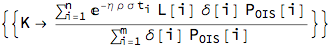
enter image description here

This is the equilibrium swap rate that will make present value at inception zero. The new formula differs from the swap rate formula in the single curve framework in two instances:

  • Discount factor P comes from a special discounting curve - the OIS curve and becomes Subscript[P, OIS][t,Subscript[T, i]]
  • Numerator does not reduce to a simple difference of two discount factors since adjusted Libor rate L[t, Subscript[T, 1],Subscript[T, 2]] E^(-t [Rho] [Eta] [Sigma]) is now estimated on a different curve, the so-called estimation curve

Caps and Floors

Consider first a Caplet paying out at time Subscript[T, k]. Caplet is essentially a call option on forward Libor rate L[t;Subscript[T, k-1],Subscript[T, k]]: [Delta][[Tau]] *(L[t;Subscript[T, k-1],Subscript[T, k]]-K)^+ where [Delta][[Tau]] is a year fraction between Subscript[T, 1] and Subscript[T, 2] and K is a fixed strike rate. The pricing formula is simply a discounted conditioned expectation of the payoff positivity under certain distributional assumptions. So, to price a Caplet in multi-curve framework, we proceed as in mono-currency case, with replacement: Libor mono-curve -> Libor multi-curve: enter image description here

Pricing formula will differ depending on the choice distributional assumptions for the forward Libor rate. For calculation purposes, we set the adjusted Libor rate -Subscript[L, e][t;Subscript[T, 1],Subscript[T, 2]] E^(-t [Rho] [Eta] [Sigma]) = x0. We choose the three processes that become the most common in the market - i.e. (i) Normal process, (ii) LogNormal process and (iii) Mean-reverting Normal process.

  • Normal process:

    nProc = OrnsteinUhlenbeckProcess[0, ?, 0, x0];
nCplt = Subscript[P, OIS][t, i] ?[i] Expectation[Max[x - k, 0],
     x \[Distributed] nProc[t], 
    Assumptions -> ? > 0 && t > 0] // FullSimplify

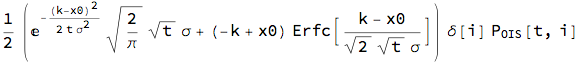
enter image description here

We can now investigate the behaviour of the Caplet w..r.t Libor volatility and strike

Plot3D[nCplt /. {Subscript[P, OIS][t, i] -> 0.98, ?[i] -> 0.25,
    x0 -> 0.0125, t -> 1}, {?, 0.005, 0.015}, {k, 0.01, 
  0.0135}, PlotLabel -> 
  Style["Caplet Normal premium", Blue, {15, Bold}], 
 PlotLegends -> Automatic, AxesLabel -> Automatic, 
 ColorFunction -> "Rainbow"]

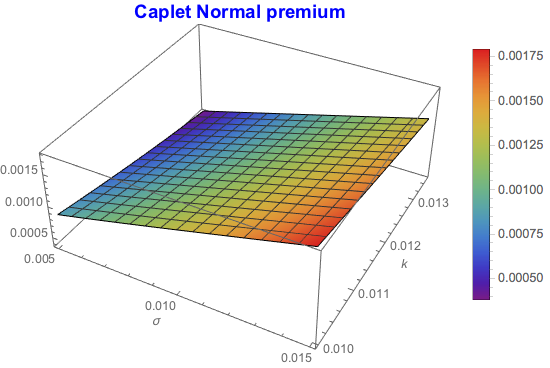
enter image description here

Premium increases as volatility goes up and strike declines. However, volatility is more dominant factor.

  • Lognormal process

    lProc = GeometricBrownianMotionProcess[0, ?, x0];
lCplt = Subscript[P, OIS][t, i] ?[i] Expectation[Max[x - k, 0],
     x \[Distributed] lProc[t], 
    Assumptions -> ? > 0 && t > 0 && k > 0 && x0 > 0] // 
  FullSimplify

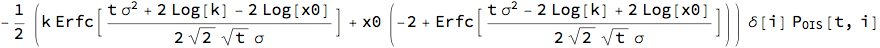
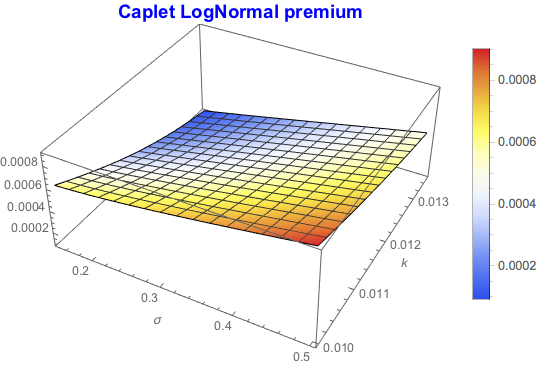
enter image description here

A similar pattern is observed for other processes, such as LogNormal

Plot3D[lCplt /. {Subscript[P, OIS][t, i] -> 0.98, ?[i] -> 0.25,
    x0 -> 0.0125, t -> 1}, {?, 0.15, 0.5}, {k, 0.01, 0.0135}, 
 PlotLabel -> Style["Caplet LogNormal premium", Blue, {15, Bold}], 
 PlotLegends -> Automatic, AxesLabel -> Automatic, 
 ColorFunction -> "TemperatureMap"]

enter image description here

  • Mean-reverting normal process

    mProc = OrnsteinUhlenbeckProcess[?, ?, ?, x0];
mCplt = Subscript[P, OIS][t, i] ?[i] Expectation[Max[x - k, 0],
     x \[Distributed] NormalDistribution[a, b], 
    Assumptions -> b > 0 && t > 0];
mCplt = % /. {a -> mProc[t][[1]], b -> mProc[t][[2]]} // FullSimplify

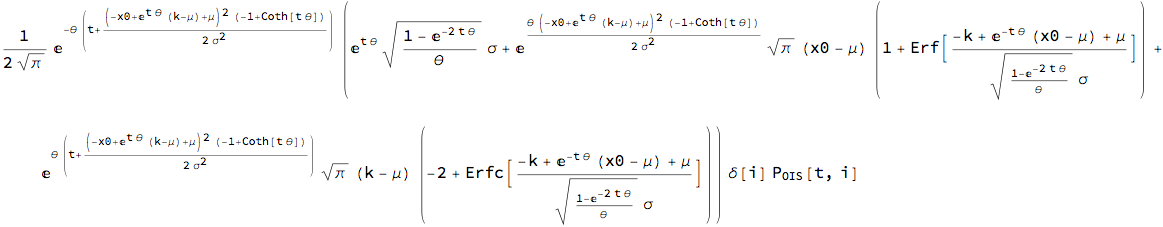
enter image description here

Floors

Interest rate floors are are essentially put options on forward Libor rate with payoff function:
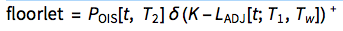
enter image description here

  • Normal process

    nProc = OrnsteinUhlenbeckProcess[0, ?, 0, x0];
nFlrt = Subscript[P, OIS][t, i] ?[i] Expectation[Max[k - x, 0],
     x \[Distributed] nProc[t], 
    Assumptions -> ? > 0 && t > 0] // FullSimplify

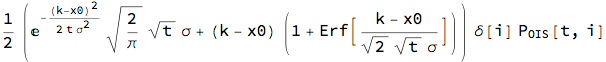
enter image description here

  • LogNormal process

    lFlrt = Subscript[P, OIS][t, i] ?[i] Expectation[Max[k - x, 0],
     x \[Distributed] lProc[t], 
    Assumptions -> ? > 0 && t > 0 && k > 0 && x0 > 0] // 
  FullSimplify

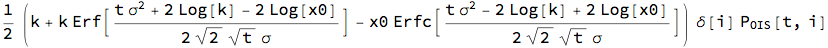
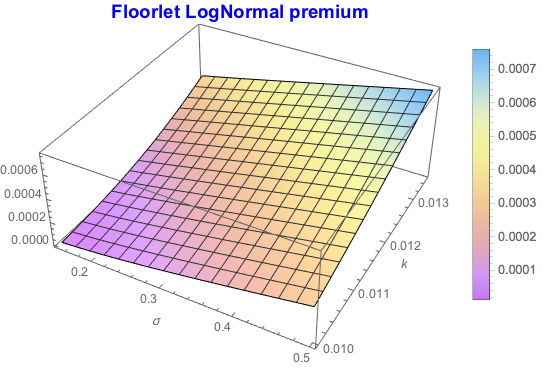
enter image description here

Plot3D[lFlrt /. {Subscript[P, OIS][t, i] -> 0.98, ?[i] -> 0.25,
    x0 -> 0.0125, t -> 1}, {?, 0.15, 0.5}, {k, 0.01, 0.0135}, 
 PlotLabel -> Style["Floorlet LogNormal premium", Blue, {15, Bold}], 
 PlotLegends -> Automatic, AxesLabel -> Automatic, 
 ColorFunction -> "Pastel"]

enter image description here

Swaptions

Swaptions are options on the swap rate defined above. They exist in tow formats: (i) Payer swaption = put option on the swap rate and (ii) Receiver swaption = call option on the swap rate. When we operate in the multi-curve framework, we deal with the same problem as in Libor case - i.e. swap rate adjustment.

We develop the swap adjustment in the same way as Libor. When LogNormal dynamics for the swap rate is envisaged, we arrive at the adjustment quantity though a joint expectation process:

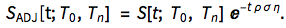
enter image description here

The volatilities in the exponent are now swaption volatilities and correlation coefficient $\rho$ is the correlation between the swap rate and the adjuster.

Receiver swaption

This is the call option on the swap rate with the payoff ; Rec_OSWP = Subscript[AF, OIS] (Subscript[S, ADJ][t; Subscript[T, 0],Subscript[T, n]] -K)^+ where:

Subscript[AF, OIS] = Sum[?[i] Subscript[P, OIS][i], {i, 1, n}]

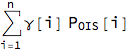
enter image description here

The option premium will depend on the modelling choice for the underlying swap rate. We look again at (i) Normal process, (ii) LogNormal process and (iii) Mean-reverting Normal process:

  • Normal process

    nSwpn = Subscript[AF, OIS]
    Expectation[Max[x - k, 0], x \[Distributed] nProc[t], 
    Assumptions -> ? > 0 && t > 0] // FullSimplify

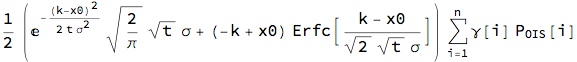
enter image description here

  • LogNormal process

    lSwpn = Subscript[AF, OIS]
    Expectation[Max[x - k, 0], x \[Distributed] lProc[t], 
    Assumptions -> ? > 0 && t > 0 && k > 0 && x0 > 0] // 
  FullSimplify

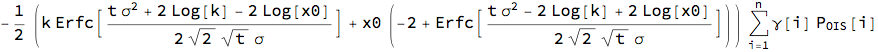
enter image description here

  • Normal mean-reverting process

    mCplt = Subscript[AF, OIS]
    Expectation[Max[x - k, 0], 
    x \[Distributed] NormalDistribution[a, b], 
    Assumptions -> b > 0 && t > 0];
mCplt = % /. {a -> mProc[t][[1]], b -> mProc[t][[2]]} // FullSimplify

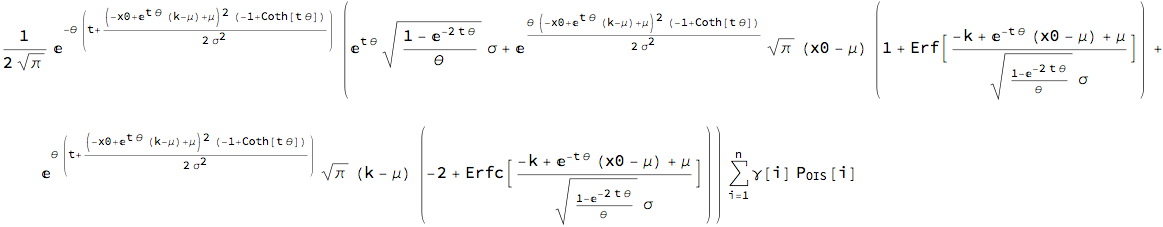
enter image description here

Payer swaption

These are put opinions on the swap rate which in case of multi-curve environment is drift-adjusted. For example, if we assume normal distribution for the swap rate, we get

  • Normal process

    nSwpn2 = Subscript[AF, OIS]
    Expectation[Max[k - x, 0], x \[Distributed] nProc[t], 
    Assumptions -> ? > 0 && t > 0] // FullSimplify

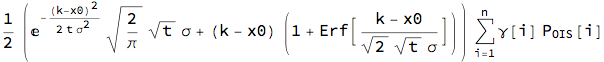
enter image description here

Conclusion

Multi-curve framework in case of interest rate derivatives brings new paradigm that requires certain adjustment to the underlying rates. This is due to a measure change when the expectation of the rates stops being martingale. Introduction of separate discounting curve - OIS requires adjustment to the forward rate drift in order to preserve non-arbitrage condition. Quarto-style adjustment known in foreign currency market is being used to derive neat formula.

Pricing and valuation adjustment with Mathematica, as the above demonstration shows, is easy. Availability of stochastic routines and probabilistic functions leads to quick and elegant solution.
POSTED BY: Igor Hlivka
3 Replies
Sort By:

As always Igor, a very well written explanation of the use of change of measure techniques for multi-curve dynamics in the evaluation of interest rate derivatives. However I am still confused about some of the details in the section Libor adjustment in multi-curve framework. In the paragraph just above the definition of cDist and cdrift , you have Subscript[E, OIS][Fe] = Subscript[E, e][Fd Bj]. In the first place Fe is defined relative to the Libor estimation curve and the measure Subscript[Q, e], so the LHS of the equation should be Subscript[E, e][Fe] which then leads to a contradiction. I think that you meant to use Fd which is measured wrt the OIS curve giving Subscript[E, OIS][Fd] = Subscript[E, e][Fd Bj] so that according to Girsanov's theorem we have the Radon-Nikodym derivative Bj = d Subscript[Q, d]/d Subscript[Q, e]. Now we can substitute for Fd with the equation Fd == Fe Aj, so that the RHS becomes Subscript[E, e][Aj Fe Bj] == Aj Subscript[E, e][Fe Bj], where Aj is the forward basis/adjustment. This is now consistent with Aj *Subscript[E, e][Fe Bj] == cdfift and the definition of Aj.

I most probably have got something mixed up, but would appreciate it if you could better explain how Subscript[E, OIS][Fe] = Subscript[E, e][Fd Bj] is consistent with the change of measure and the definitions for cdrift and Aj.

Regards Michael
POSTED BY: Michael Kelly

Thank you, Michael, for your comments and observations.

The first equation you refer to shows the 'translation' of forward rate estimation (Libor) from OIS-driven measure = 'discount' measure to the one driven by the forward measure where 'adjusted' Libor is martingale. The equation was meat to show that Libor estimation (on the Libor) curve but discounted on a different OIS curve was identical to OIS forward time adjustment factor when the estimation was done with the forward probability measure. This was to demonstrate that Libor is essentially a function of the OIS forward rate time adjustment.

Subscript d or OIS describes the estimation using discounting curve (OIS curve), whereas subscript e denotes the estimation under the forward curve. The term E(OIS) [Fe} was meat to show Libor rate estimation with OIS curve discounting - i.e. Libor rate with different discounting curve (i.e. in multi-curve framework). Indeed, the expression should have read Fd - as you suggested.

Your comment makes this exposition now more clearer and explicit and also corrects the statement I meant to present. Thank you for spotting it and for making it theoretically justified. This is appreciated!

Best Igor
POSTED BY: Igor Hlivka

enter image description here - Congratulations! This post is now a Staff Pick as distinguished by a badge on your profile! Thank you, keep it coming!

POSTED BY: EDITORIAL BOARD
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract