Group Abstract Group Abstract

Message Boards Message Boards

Visualizing Euler's Formula

A previous post caused me to think about how to visualize Euler's Formula Exp[ i Pi ] = -1. I use a (slowly) converging series for Pi.

 t[n_] = (4 (-1)^n)/(2 n + 1);

Sum[t[n], {n, 0, \[Infinity]}] - \[Pi]

0

Calculating the exponent of i times the sum of the series for an increasing number of terms gives me a plot which converges toward -1

se = {Re[#], Im[#]} & /@ 
   Table[Exp[I Sum[t[n], {n, 0, m}]], {m, 0, 1000}];

ListPlot[se, Joined -> True]
POSTED BY: Frank Kampas
6 Replies
Sort By:

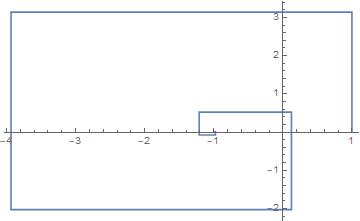
One can also do the series of expansion of e^(i pi)

ListPlot[Table[ReIm[Sum[(I \[Pi])^n/n!, {n, 0, m}]], {m, 0, 10}], 
 Joined -> True]

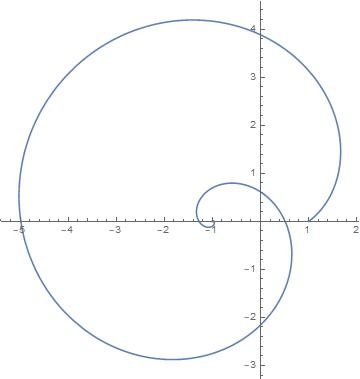
enter image description here

or a ParametricPlot of the evaluated form

ParametricPlot[
 Evaluate[ReIm[Sum[(I \[Pi])^n/n!, {n, 0, m}]]], {m, 0, 20}, 
 PlotRange -> All]

enter image description here
POSTED BY: Frank Kampas

Evaluating f generates a continuous function, which is why ParametricPlot can do a plot.

In[12]:= Evaluate[f[x]]

Out[12]= {Re[E^(I (\[Pi] + 2 (-1)^x LerchPhi[-1, 1, 3/2 + x]))], 
 Im[E^(I (\[Pi] + 2 (-1)^x LerchPhi[-1, 1, 3/2 + x]))]}

Our plots agree for integer arguments of f

enter image description here
POSTED BY: Frank Kampas

I don't understand how ParametricPlot can work for a function which only evaluates for integer arguments. When I look at the entire plot using PlotRange -> All I get enter image description here
POSTED BY: Frank Kampas

Hello Frank

I checked and it works fine on MMA 10.2(11.2) version.

I don't know how ParametricPlot can work, maybe one of the WRI/SE jedi can join the party to provide even more insights on this.

Regards Mariusz.
POSTED BY: Mariusz Iwaniuk

Great!!!

My try:

t[n_] := (4 (-1)^n)/(2 n + 1);
f[m_] := ReIm[Exp[I Sum[t[n], {n, 0, m}]]];
ParametricPlot[Evaluate[f[m]], {m, 0, 50}, PlotRange -> Full]

enter image description here
POSTED BY: Mariusz Iwaniuk

enter image description here
POSTED BY: Frank Kampas
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard