I have been trying to solve the following equations(Eq.1) in cylinder coordinates. And I want my solution domain is r>=0. Because of the 1/r and 1/r^2 terms in Eq.1, I ran into the Infinity error problem when using NDSolve . Then I rewrote my equations by multiplying them by r or r^2 to remove 1/r and 1/r^2 terms and got Eq.2, but I still met the Infinite problem using NDSolve. So is it possible to get solutions if my solution domain is r>=0. I believe this solution is physically real but I do not know how to get it using NDSolve. Any help would be great. 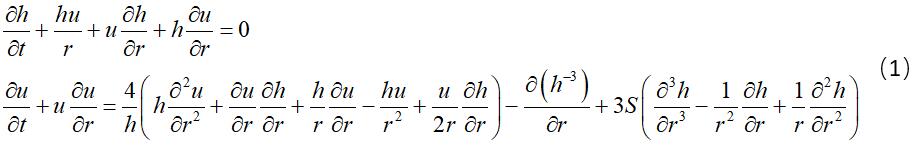
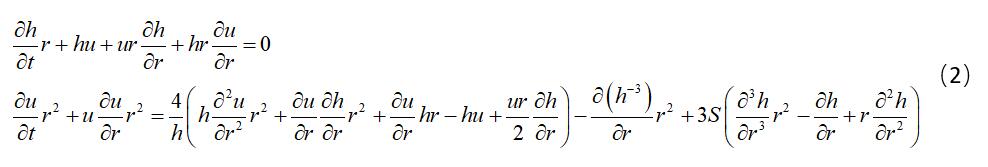
And my codes for Eq.2 are:
TMax = 1.615; S = 1/Pi^2/2; rMin = 0; rMax = 2;
{usol, hsol} =
NDSolveValue[{D[u[t, r], t]*r^2 == -D[u[t, r], r]*u[t, r]*r^2 +
3*1/h[t, r]^4*D[h[t, r], r]*r^2 +
3*S*(D[h[t, r], r, r, r]*r^2 - D[h[t, r], r] +
r*D[h[t, r], r, r]) +
4/h[t, r]*(h[t, r]*r^2*D[u[t, r], r, r] +
D[u[t, r], r]*D[h[t, r], r]*r^2 + h[t, r]*r*D[u[t, r], r] -
h[t, r]*u[t, r] - u[t, r]*r/2*D[h[t, r], r]),
D[h[t, r], t]*r == -h[t, r]*u[t, r] - u[t, r]*r*D[h[t, r], r] -
h[t, r]*r*D[u[t, r], r], u[0, r] == 0,
h[0, r] == 1 - 0.2*Cos[Pi*r], h[t, rMin] == h[t, rMax]}, {u,
h}, {t, 0, TMax}, {r, rMin, rMax}, PrecisionGoal -> Infinity,
AccuracyGoal -> 10, MaxSteps -> 10^6,
Method -> {"MethodOfLines",
"SpatialDiscretization" -> {"TensorProductGrid",
"MaxPoints" -> 5000, "MinPoints" -> 5000,
"DifferenceOrder" -> 4}}]