Group Abstract Group Abstract

Message Boards Message Boards

Draw 2D Hexagon to 3D Hexagon prism, or Thick Hexagon Mesh?

Arm Mo
Posted 7 years ago
Attachments:
POSTED BY: Arm Mo
5 Replies
Sort By:
Aaron Gerst
Aaron Gerst
Posted 7 years ago

Thx Henrik, the best solution 1 1

POSTED BY: Aaron Gerst

hi, I would like to knoww how do I elaborate a fractal hexagon including manipulate. Help me please.
POSTED BY: Ana Sofia Trejos Vanegas

Ok, ok, you are absolutely right! Here comes a somewhat cleaner solution:

hexPts[x_, y_] := Table[{Cos[2 Pi k/6] + x, Sin[2 Pi k/6] + y}, {k, 7}]
hexConns[x_, y_] := Partition[hexPts[x, y], 2, 1]
wall[h_][{{x1_, y1_}, {x2_, y2_}}] := Polygon[{{x1, y1, 0}, {x2, y2, 0}, {x2, y2, h}, {x1, y1, h}}]
hex3D[h_][x_, y_] := wall[h] /@ hexConns[x, y]
Graphics3D[Table[hex3D[2][3 i + 3 ((-1)^j + 1)/4, Sqrt[3]/2 j], {i, 10}, {j, 15}]]

This now gives:

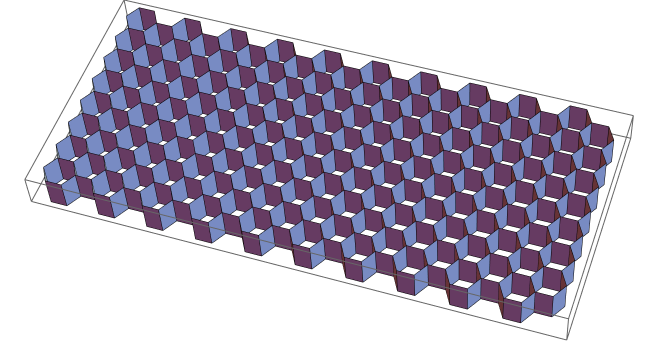
enter image description here

The hight of the hexagons can be chosen individually:

Graphics3D[Table[hex3D[RandomReal[3]][3 i + 3 ((-1)^j + 1)/4, Sqrt[3]/2 j], {i, 10}, {j, 15}]]

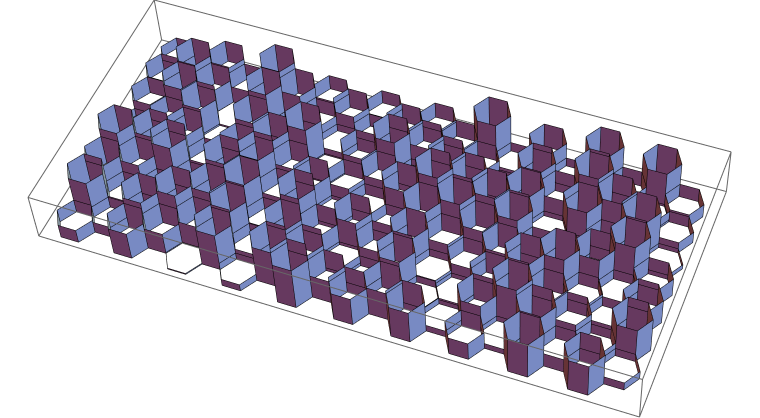
enter image description here

Hope that helps, regards -- Henrik
POSTED BY: Henrik Schachner

Here comes just a "quick and dirty" option - but short at least:

h3D[x_, y_, r_] := Tube[Table[{Cos[2 Pi k/6] + x, Sin[2 Pi k/6] + y, 0}, {k, 7}], r]
Graphics3D[{Table[h3D[3 i + 3 ((-1)^j + 1)/4, Sqrt[3]/2 j, .3], {i, 10}, {j, 15}]}]

which gives:

enter image description here

Regards -- Henrik
POSTED BY: Henrik Schachner
Arm Mo
Arm Mo
Posted 7 years ago

Thanks a lot, but this is not what I want. I want the 3D Hexagon Prisms. Or at least is there away to modify this to change from round tubes to 3d hexagons packed next to each other ?

POSTED BY: Arm Mo
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard