Introduction

The new version of Mathematica (11.3) introduces a whole range of interesting new functionality. Some functions like FindTextualAnswer and FindEquationalProof quite clearly open up new possibilities and provide tools of enormous power. But MMA 11.3 also introduces a huge range of other functionality that might go a bit unnoticed but also is highly interesting. Here I show the example of DeBruijnSequence and DeBruijnGraph which are interesting not only for safe busters.

Suppose we have a lock like this one:

Suppose we have to enter a 4 digit code. There are $10^4=10000$ combinations, starting at 0000, 0001, ..., 9999. Each has 4 digits so if I want to test all combinations I will need 40000 keystrokes.

Let's suppose that the key lock is stupid, and only remembers the last for digits you entered. So if you entered 207689, it would have tested the combinations 2076, 0768, and 7689. So I only needed to type in 6 keystrokes instead of 12. We want to ask the following question:

What is the shortest sequence of digits (keystrokes) that will contain all possible combination of 4 digits as subsequences?

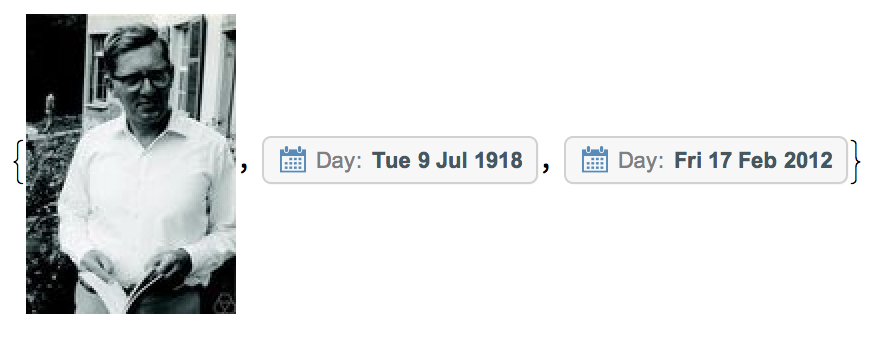
The answer is given by the DeBruijnSequence, named after the Dutch mathematician Nicolaas Govert (Dick) de Bruijn (9 July 1918 – 17 February 2012).

Entity["Person", "NicolaasGovertDeBruijn::3s54p"][{"Image", "BirthDate", "DeathDate"}]

As my explanation of the problem is not good, I recommend this video where someone explains the whole thing much better than me.

A simpler problem

Let's make the whole problem a bit simpler. Suppose I only have two digits 1 and 2 and I want to find all possible combinations of 2.

Tuples[{1, 2}, 2]
(*{{1, 1}, {1, 2}, {2, 1}, {2, 2}}*)

So there are 4 tuples of length 2, which require me to type in 8 keystrokes. Let's see if we can do better if the lock remembers only the last for digits entered. The sequence

1, 1, 2, 2,1

solves this problem. If I partition it and always shift by one I get:

Partition[{1, 1, 2, 2, 1}, 2, 1]
(*{{1, 1}, {1, 2}, {2, 2}, {2, 1}}*)

All combinations of subsequences. It turns out that the sequence 1,1,2,2,1 is a DeBruijnSequence:

DeBruijnSequence[{1, 2}, 2]
(*{1, 1, 2, 2}*)

Note that I have to read the sequence cyclically, i.e. when I reach the end I have to keep typing (length of required sequences)-1 digits from the beginning. In this case the length the subsequences is 2 so I need to add the first digit to the end:

1,1,2,2,1

How can we find such a sequence? Well, one way is to write down all the tuples of two digits:

Tuples[{1, 2}, 2]
(*{{1, 1}, {1, 2}, {2, 1}, {2, 2}}*)

We then look for "overlapping sequences". So for example takes the first element of the tuple list {1,1}, delete its first entry {1} and then take all list that you can construct by adding one digit to the end: {1,1} and {1,2}. This gives two links in a graph {1,1}->{1,1} and {1,1}->{1,2}. We then proceed like that for all other tuples, i.e. we link them to those tuples that can be generated by deleting the first entry and adding any of the available digits:

DeleteCases[Flatten[Outer[If[Drop[#1, 1] == Drop[#2, -1], #1 -> #2] &, tuples, tuples, 1], 1], Null]
(*{{1, 1} -> {1, 1}, {1, 1} -> {1, 2}, {1, 2} -> {2, 1}, {1, 2} -> {2, 2}, {2, 1} -> {1, 1}, {2, 1} -> {1, 2}, {2, 2} -> {2, 1}, {2, 2} -> {2, 2}}*)

The respective graph looks like this:

g = Graph[DeleteCases[Flatten[Outer[If[Drop[#1, 1] == Drop[#2, -1], #1 -> #2] &, tuples, tuples, 1], 1], Null], PlotTheme -> "Scientific"]

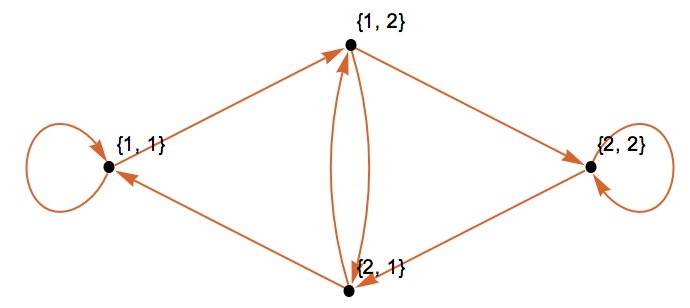
Next we need to find a HamiltonianPath, i.e. a path that visits every note exactly once:

hamiltonpath = FindHamiltonianPath[g]
(*{{1, 1}, {1, 2}, {2, 2}, {2, 1}}*)

The rule to construct the DeBruijnSequence is then easy. We use the first entry of the path, i.e. {1,1} and then add one by one the second elements of all tuples in the list:

sequence = Join[hamiltonpath[[1]], hamiltonpath[[2 ;;, 2]]]
(*{1, 1, 2, 2, 1}*)

Note that the DeBruijnSequence that Mathematica gives is one shorter, i.e. cyclic, ours just reconstructed sequence is not!

The Wolfram Language also has a function that directly constructs the Graph:

DeBruijnGraph[2, 2, PlotTheme -> "Scientific"]

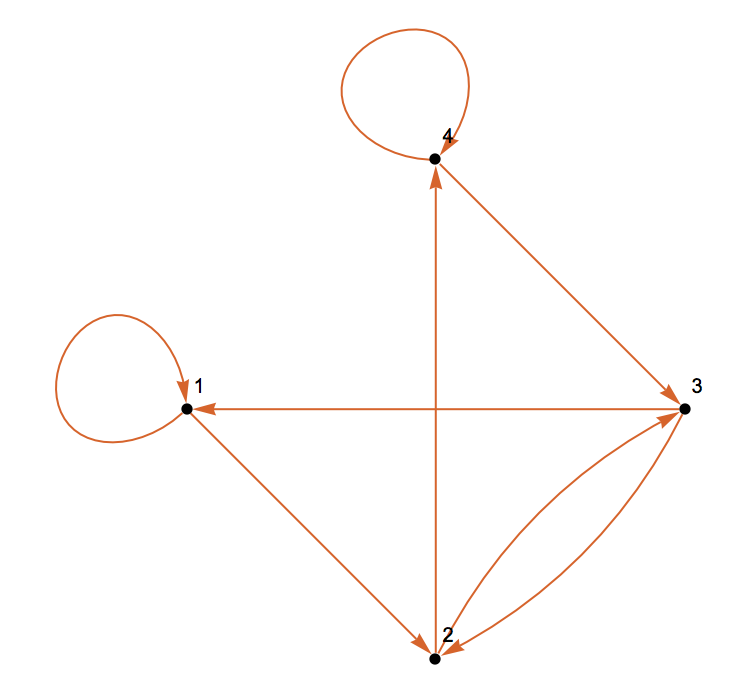
This graph looks different from the one we constructed above, but this is just its layout. In fact the graphs are isomorphic:

IsomorphicGraphQ[DeBruijnGraph[2, 2], g]

evaluates to "True".

A slightly more complicated example

Ok. Let's do one more example. We are looking for sequences of length 2 on an alphabet of three digits, 1,2, and 3.

tuples = Tuples[{1, 2, 3}, 2];
g = Graph[DeleteCases[Flatten[Outer[If[Drop[#1, 1] == Drop[#2, -1], #2 -> #1] &, tuples, tuples, 1], 1], Null], PlotTheme -> "Scientific"]

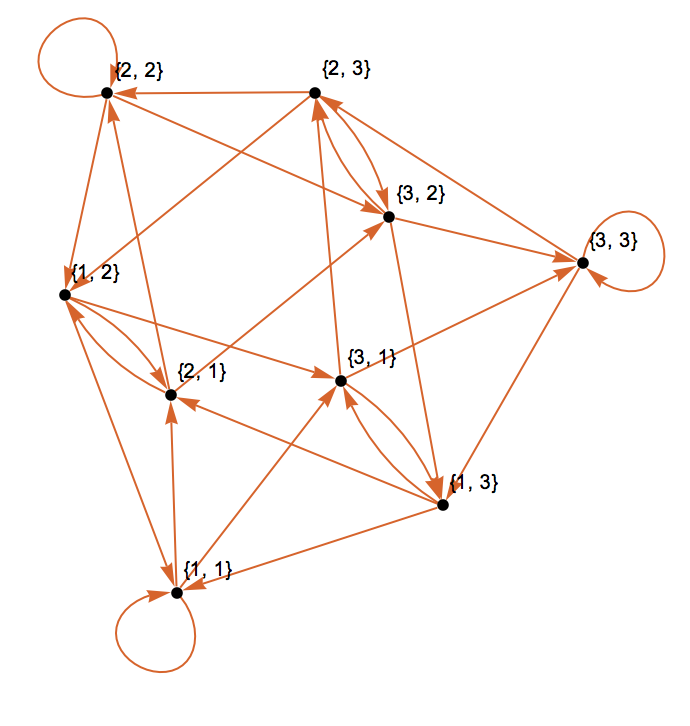
which turns out to be isomorphic to

DeBruijnGraph[3, 2, PlotTheme -> "Scientific"]

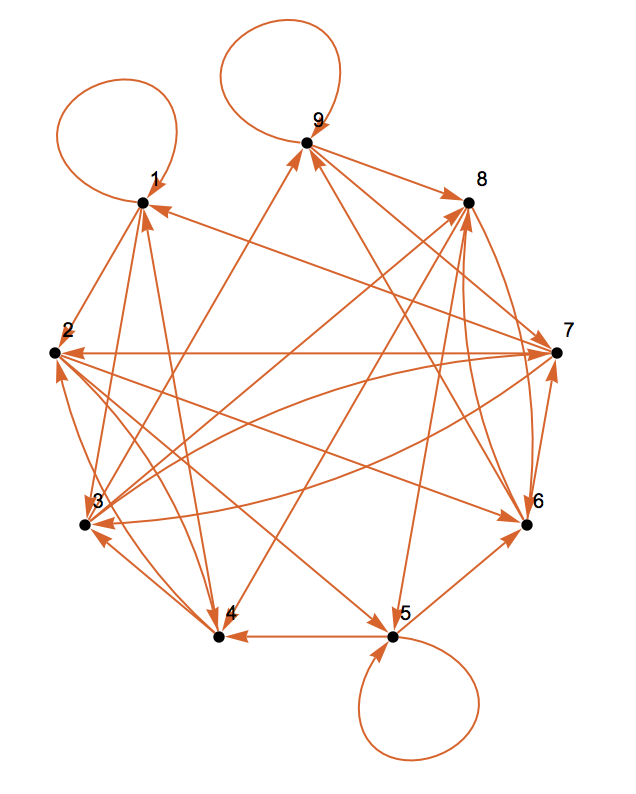
so that

IsomorphicGraphQ[DeBruijnGraph[3, 2], g]

gives "True".

Solution to our problem

We are not ready to solve our key lock problem. We are looking for the DeBruijnSequence for string length 4 and on the 10 digits 0,1,2,...,9.

DeBruijnSequence[10, 4]

The sequence is

DeBruijnSequence[10, 4] // Length

10000 long, but it's cyclic so we have to add the first three digits to the end to have all combinations. This means that 10003 keystrokes are enough, which has just saved us nearly 30000 keystrokes!!!! This is fantastic if you want to bust a safe.

For those interested: here is the explanation by a professional.

Note, that this is quite useful for DNA sequencing, too.

Extending the DeBruijnSequence to more dimensions

Of course, a mathematician always asks whether we can generalise this. Let's try to generate a two dimensional DeBruijn sequence, i.e. a torus instead of a cycle like before (remember that the sequence that the Wolfram Langauge generates has to be considered to be cyclic!). Again you can find the main idea on this website.

It turns out that there is, of course, maths for this: Toroidal tilings from de Bruijn-Good cyclic sequences. The algorithm is a bit technical, but at the end we obtain:

deBruijn2D[symbols_, l_, w_] := 
Module[{column1, shifts, solution}, 
column1 = DeBruijnSequence[symbols , l]; 
shifts = DeBruijnSequence[symbols^l, w - 1]; 
solution = Transpose[FoldList[RotateLeft, column1, shifts][[;; -2]]]; 
If[EvenQ[symbols] && w == 2, Join[#, {#[[1]]}] &@Transpose[Join[Transpose[solution], {RotateLeft[Transpose[solution][[1]], 1/2 symbols^l]}]], 
Join[#, {#[[1]]}] &@Transpose[Join[Transpose[solution], {Transpose[solution][[1]]}]]]]

The input slots are:

• symbols : number of different symbols (will be represented as digits starting at zero.
• length: length of the sequences; similar to the one dimensional case ("of length 4").
• width: similar to length but for the second direction; refer to paper.

In fact if length_ is m, width_ is n and we have an alphabet of c numbers, then we obtain an array of size: $c^m \times c^{m(n-1)}$. So here is the DeBruijn tiling in two dimensions, on two digits where the length and width are both 2.

deBruijn2D[2, 2, 2] // MatrixForm

Here is a more colourful representation:

ArrayPlot[deBruijn2D[2, 2, 2] /. {0 -> Red, 1 -> Green}]

This is actually quite useful. Every 2 by 2 square is unique in the plane and all combinations occur. This means that if I know the colours of the tiles in one 2 by 2 square I know where I am on the plane!!!!

More symbols/larger systems

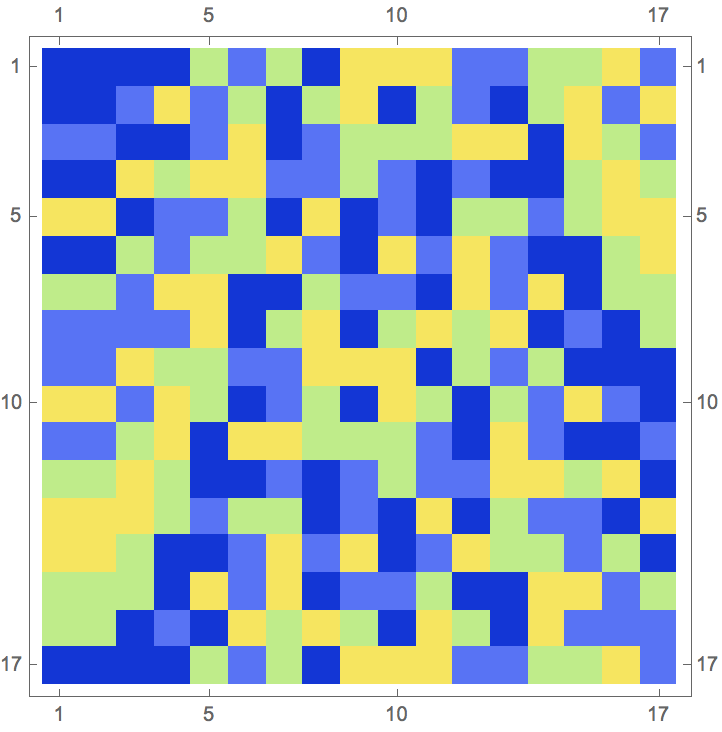
Let's look at a system with 4 symbols and 2 by 2 square tiles.

solution=deBruijn2D[4, 2, 2]

Here is a nice representation of that (in which I have "added" a column/row to take care of the cyclicity):

Grid[Partition[Grid /@ Flatten[Partition[solution /. {0 -> White, 1 -> Green, 2 -> Blue, 3 -> Red}, {2, 2}, 1], 1], 16], Frame -> All]

Modulo bugs in my code, each of these 2-by-2 squares should be "unique". There should be $4^4=256$ different 2-by-2 tiles:

Length[Flatten[Partition[solution2, {2, 2}, 1], 1] // DeleteDuplicates]

gives 256, which is a good sign. Here is another representation without the black grid (which is also non-cyclic):

ImageAssemble[(Graphics[{#, Rectangle[]}] & /@ #) & /@ (solution/. {0 -> White, 1 -> Green, 2 -> Blue, 3 -> Red})]

Of course, everything actually lives on a torus:

imgtiles = ImageAssemble[(Graphics[{#, Rectangle[]}] & /@ #) & /@ (solution[[;; -2]][[All, ;; -2]] /. {0 -> White, 1 -> Green, 2 -> Blue, 3 -> Red})];
img = ImageResize[imgtiles, 775];
imgmatrix = Join[ImageData[img], ImageData[img]];
frames = Table[
ParametricPlot3D[{Cos[u] (3 + Cos[v]), Sin[u] (3 + Cos[v]), Sin[v]}, {u, 0, 2 \[Pi]}, {v, 0, 2 \[Pi]}, 
TextureCoordinateFunction -> ({ #4,  #5} &), PlotStyle -> Directive[Specularity[White, 50], Texture[Image[imgmatrix[[g ;; g + 774, All, All]]]]], 
Axes -> False, Lighting -> "Neutral", Mesh -> None, Boxed -> False, ImageSize -> 900], {g, 1, 775, 7}];
Do[Export["~/Desktop/DeBruijnTorus/frame" <> ToString[1000 + i] <> ".jpg", frames[[i]]], {i, 1, Length[frames]}]

Automatic graphics

We can create another function for the visualisation:

deBruijnPlot[matrix_] := Module[{}, (MatrixPlot[# /. (Rule @@@ Transpose[{#, RandomColor[Length[#]]}] &@
DeleteDuplicates[Sort[Flatten[#]]])]) &@matrix ]

So we get:

deBruijnPlot[deBruijn2D[4, 2, 2]]

Conclusion

DeBruijnSequences are very intriguing mathematical objects with many applications. Here is for example a card trick based on the DeBruijnSequence. They can help to sequence DNA and to know where you are on a plane if all you have is very local information.

The functions that I introduced in this post are not optimised at all. They are relatively slow, and you will have to respect certain rules for length and width. Also the size of the matrices increases very fast as the number of symbols, length and width increase. Some slightly larger systems than the ones shown in the post can be computed, however, and their patterns are intriguing:

deBruijnPlot[deBruijn2D[8, 3, 2]]

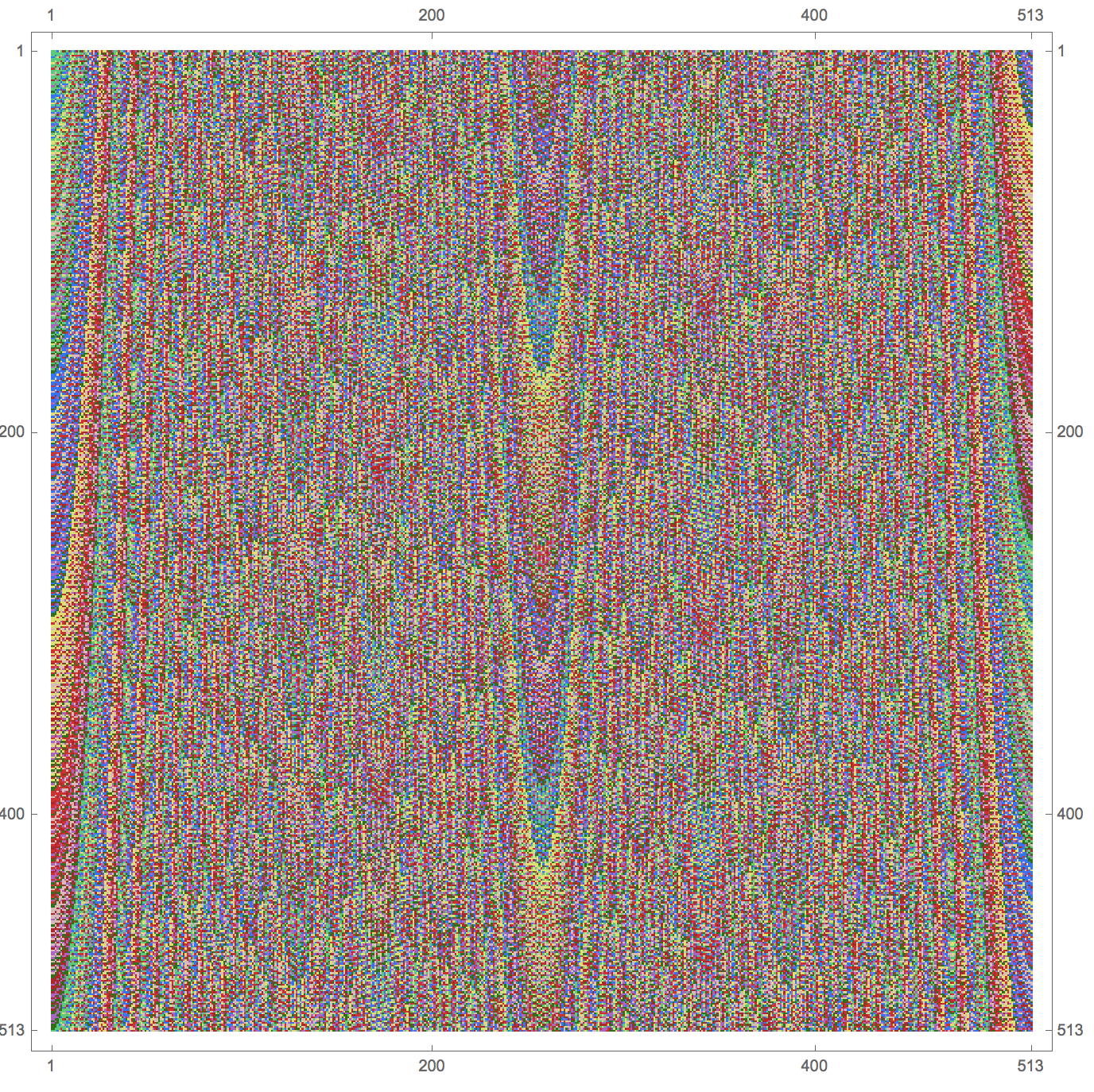
They are obviously a consequence of the algorithm that I have used.

It is also quite possible to extend the entire procedure to more than 2 dimensions, but that is for another day....

Cheers,

Marco