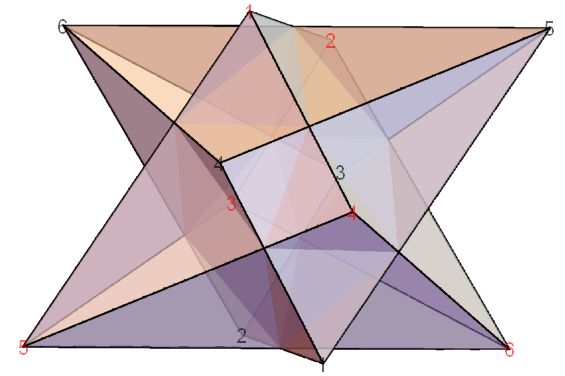
The weirdest of the seven hexahedra, the tetragonal antiwedge, is a self-dual polyhedron that has a volume of 3.141 in its canonical form. Here it is shown with its dual.
Here's code for it.
verts={
{Root[-1+14 #1^2+25 #1^4-8 #1^6+#1^8&,1],1,Root[-1-14 #1^2+25 #1^4+8 #1^6+#1^8&,2]},
{Root[-1+14 #1^2+25 #1^4-8 #1^6+#1^8&,2],1,-Root[-1-14 #1^2+25 #1^4+8 #1^6+#1^8&,2]},
{-Root[-1+10 #1^2-31 #1^4+80 #1^6+#1^8&,2],-Root[1-8 #1-2 #1^2-8 #1^3+#1^4&,1],-Root[-1+6 #1^2-15 #1^4+8 #1^6+#1^8&,2]},
{Root[-1+10 #1^2-31 #1^4+80 #1^6+#1^8&,2],-Root[1-8 #1-2 #1^2-8 #1^3+#1^4&,1],Root[-1+6 #1^2-15 #1^4+8 #1^6+#1^8&,2]},
{Root[-1-2 #1^2+5 #1^4-4 #1^6+#1^8&,1],-1,Root[-1+2 #1^2+5 #1^4+4 #1^6+#1^8&,2]},
{Root[-1-2 #1^2+5 #1^4-4 #1^6+#1^8&,2],-1,-Root[-1+2 #1^2+5 #1^4+4 #1^6+#1^8&,2]}};
dualverts = {-1,-1,1}#&/@verts;
faces={{1,2,6,4},{1,5,3,2},{1,4,5},{2,3,6},{3,5,6},{4,6,5}};
Graphics3D[{Opacity[.6],EdgeForm[{Black, Thick}],
Polygon[verts[[#]]]&/@faces,Polygon[dualverts[[#]]]&/@faces,
Table[Style[Text[n,verts[[n]]],20],{n,1,6}],Red,Table[Style[Text[n,dualverts[[n]]],20],{n,1,6}]},
ImageSize-> {600,400}, ViewAngle-> Pi/12,ViewPoint-> {0,0,3},Boxed-> False, SphericalRegion-> True]
Volume[ConvexHullMesh[verts]]
3.141058533942126`
In the canonical form, all faces are planar and all edges are tangent to the unit sphere. Combined with the dual, all edges are perpendicular with an intersection at distance 1 from the origin.