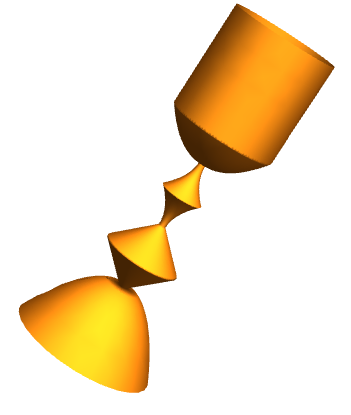A simple way is to write in Piecewise than combine in Show.
ClearAll["Global`*"]; Remove["Global`*"]
f[x_] := Piecewise[{{Sqrt[-x + 1], 0 <= x <= 1}, {-1 + x,
1 <= x <= 3/2}, {2 - x, 3/2 <= x <= 2}, {-1 + x/2,
2 <= x <= 5/2}, {3/2 - x/2, 5/2 <= x <= 3}, {Sqrt[x - 3],
3 <= x <= 7/2}, {1/Sqrt[2], 7/2 <= x <= 5}}];
f2[x_] :=
Piecewise[{{Sqrt[-x + 1.05], 0 <= x <= 1}, {(x - 1)^2 + 0.05,
1 <= x <= 3/2}, {(x - 2)^2 + 0.05,
3/2 <= x <= 2}, {(x - 2)^2 + 0.05,
2 <= x <= 5/2}, {(x - 3)^2 + 0.05,
5/2 <= x <= 3}, {Sqrt[x - 3] + 0.05,
3 <= x <= 7/2}, {1/Sqrt[2] + 0.05, 7/2 <= x <= 5}}];
f3[x_] :=
Piecewise[{{Sqrt[-x + 1.05], 0 <= x <= 1}, {(x - 1)^3 + 0.05,
1 <= x <= 3/2}, {(x - 3/2)^3 + 0.05,
3/2 <= x <= 2}, {(x - 2)^2 + 0.05,
2 <= x <= 5/2}, {(x - 3)^2 + 0.05,
5/2 <= x <= 3}, {Sqrt[x - 3] + 0.05,
3 <= x <= 7/2}, {1/Sqrt[2] + 0.05, 7/2 <= x <= 5}}];
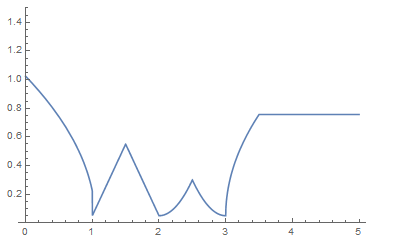
f4[x_] :=
Piecewise[{{Sqrt[-x + 1.05], 0 <= x <= 1}, {(x - 1) + 0.05,
1 <= x <= 3/2}, {-(x - 2) + 0.05,
3/2 <= x <= 2}, {(x - 2)^2 + 0.05,
2 <= x <= 5/2}, {(x - 3)^2 + 0.05,
5/2 <= x <= 3}, {Sqrt[x - 3] + 0.05,
3 <= x <= 7/2}, {1/Sqrt[2] + 0.05, 7/2 <= x <= 5}}];
Ln[x_] := Log[x];
f5[x_] :=
Piecewise[{{-Surd[x - 1, 3], 0 <= x <= 1}, {Exp[(x - 1)^2] - 0.95,
1 <= x <= 3/2}, {Exp[-(x - 1/2)^2] - 0.05,
3/2 <= x <= 2}, {(x - 2)^2 + 0.05,
2 <= x <= 5/2}, {(x - 3)^2 + 0.05,
5/2 <= x <= 3}, {Exp[(x - 3)^2] - 0.95,
3 <= x <= 3 + Sqrt[Ln[39/20]]}, {1,
3 + Sqrt[Ln[39/20]] <= x <= 6}}];
Plot[f4[x], {x, 0, 5}, PlotRange -> {Automatic, {0, 3/2}}, Exclusions -> None]
RevolutionPlot3D[f[x], {x, 0, 5}, RevolutionAxis -> {1, 0, 0},
Mesh -> None, Axes -> False, Boxed -> False, Exclusions -> None,
MaxRecursion -> 5]
RevolutionPlot3D[f2[x], {x, 0, 5}, RevolutionAxis -> {1, 0, 0},
Mesh -> None, Axes -> False, Boxed -> False, Exclusions -> None,
MaxRecursion -> 5]
RevolutionPlot3D[f3[x], {x, 0, 5}, RevolutionAxis -> {1, 0, 0},
Mesh -> None, Axes -> False, Boxed -> False, Exclusions -> None,
MaxRecursion -> 5]
RevolutionPlot3D[f4[x], {x, 0, 5}, RevolutionAxis -> {1, 0, 0},
Mesh -> None, Axes -> False, Boxed -> False, Exclusions -> None,
MaxRecursion -> 5]
RevolutionPlot3D[f5[x], {x, 0, 6}, RevolutionAxis -> {1, 0, 0},
Mesh -> None, Axes -> False, Boxed -> False, Exclusions -> None,
MaxRecursion -> 5]