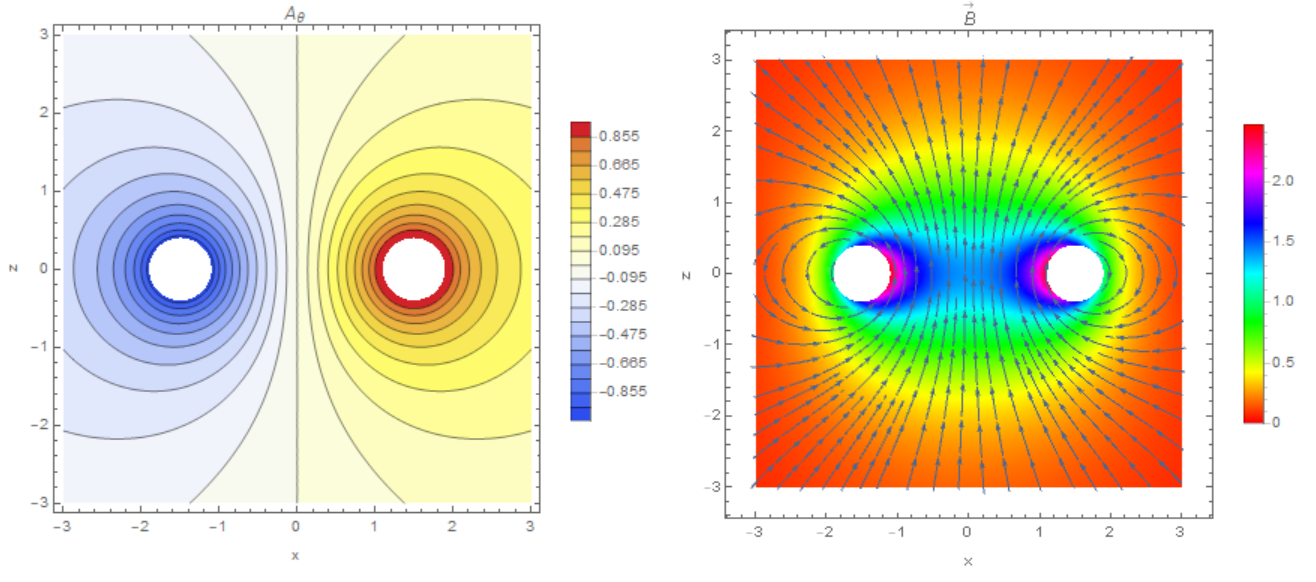
Let consider the case when there is a current in a circular loop, the vector potential has in cylindrical coordinate system only one component depending on the radial coordinate and on the coordinate z . Than we have the following model:
L1 = 6; L2 = 6; R1 = 1.5; L3 = 3; R2 = .4;
Subscript[\[ScriptCapitalR], 1] =
ImplicitRegion[y^2 + (x - R1)^2 < R2^2, {x, y}];
Subscript[\[ScriptCapitalR], 2] =
ImplicitRegion[y^2 + (x + R1)^2 < R2^2, {x, y}];;
Subscript[\[ScriptCapitalR], 3] =
RegionUnion[Subscript[\[ScriptCapitalR], 1],
Subscript[\[ScriptCapitalR], 2]];
Subscript[\[ScriptCapitalR], 4] =
ImplicitRegion[-L1 <= x <= L1 && -L2 <= y <= L2, {x,
y}]; Subscript[\[ScriptCapitalR], 5] =
ImplicitRegion[-L3 <= x <= L3 && -L3 <= y <= L3, {x,
y}]; \[ScriptCapitalR]p =
RegionDifference[Subscript[\[ScriptCapitalR], 5],
Subscript[\[ScriptCapitalR], 3]];
\[ScriptCapitalR] =
RegionDifference[Subscript[\[ScriptCapitalR], 4],
Subscript[\[ScriptCapitalR], 3]];
Us = NDSolveValue[{x*x*\!\(
\*SubsuperscriptBox[\(\[Del]\), \({x, y}\), \(2\)]\(u[x, y]\)\) == -x*
D[u[x, y], x] + u[x, y],
DirichletCondition[u[x, y] == 1, y^2 + (x - R1)^2 == R2^2],
DirichletCondition[u[x, y] == -1, y^2 + (x + R1)^2 == R2^2]},
u, {x, y} \[Element] \[ScriptCapitalR],
Method -> {"FiniteElement",
"MeshOptions" -> {"MaxCellMeasure" -> 0.0005}}]
H = {-D[Us[x, y], y], D[Us[x, y], x] + Us[x, y]/x}; {ContourPlot[Us[x, y], {x, y} \[Element] \[ScriptCapitalR]p,
Contours -> 20, FrameLabel -> {"x", "z"}, PlotRange -> All,
PlotLabel -> "\!\(\*SubscriptBox[\(A\), \(\[Theta]\)]\)",
PlotLegends -> Automatic, ColorFunction -> "TemperatureMap",
PlotPoints -> 50],StreamDensityPlot[H, {x, y} \[Element] \[ScriptCapitalR]p,
PlotRange -> All,
PlotLabel -> "\!\(\*OverscriptBox[\(B\), \(\[Rule]\)]\)",
FrameLabel -> {"x", "z"}, AspectRatio -> Automatic,
StreamPoints -> Automatic, StreamScale -> Automatic,
ColorFunction -> Hue, PlotLegends -> Automatic]}