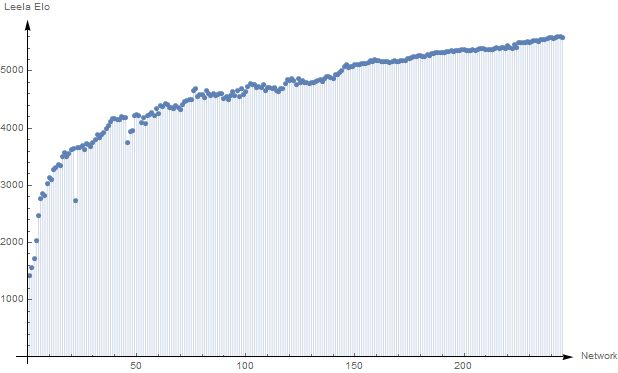
LC0 is an artificial intelligence chess engine in the spirit of alpha zero. Here is the improvement of elo performance (http://162.217.248.187/networks) The list is imported into Mathematica and visualized.
elo = Reverse[{5582.24, 5599.02, 5595.76, 5587.37, 5575.35, 5578.86,
5578.41, 5559.51, 5558.62, 5547.21, 5544.44, 5520.53, 5525.25,
5529.51, 5512, 5506.45, 5512.17, 5506.03, 5499.74, 5501.1,
5501.53, 5403.39, 5465.7, 5390.71, 5408.78, 5449.13, 5393.27,
5405.26, 5402.22, 5396.25, 5405.12, 5388.28, 5373.22, 5373.22,
5382.08, 5376.9, 5389.56, 5385.24, 5388.75, 5377.15, 5362.19,
5372.96, 5358.95, 5361.91, 5362.32, 5373.95, 5371.42, 5357.75,
5364.27, 5356.47, 5339.32, 5359.03, 5341.32, 5345.33, 5320.59,
5322.68, 5323.93, 5329.32, 5323.33, 5308.89, 5297.69, 5270.72,
5284.89, 5252.59, 5260, 5276.7, 5267.33, 5260.23, 5246.83, 5235.3,
5220.19, 5213.11, 5191.5, 5182.34, 5176.54, 5160.91, 5174,
5179.87, 5169.23, 5155.79, 5160.24, 5162.81, 5169.7, 5160.77,
5180.88, 5186.43, 5193.7, 5160.59, 5186.78, 5140.89, 5137.88,
5134.54, 5127.34, 5116.73, 5121.87, 5120.67, 5071.68, 5073.65,
5062.54, 5105.09, 5079.68, 5012.99, 4968.4, 4944.51, 4931.96,
4865.13, 4893.65, 4902.49, 4897.91, 4867.15, 4817.83, 4847.71,
4828.7, 4815.66, 4790.06, 4803.49, 4783.36, 4805.28, 4806.17,
4828.25, 4794.17, 4871.79, 4766.88, 4838.96, 4861.16, 4827.88,
4843.98, 4779.94, 4686.33, 4694.95, 4635.64, 4662.68, 4710.17,
4691, 4714.87, 4707.12, 4666.22, 4770.97, 4714.4, 4723.58,
4717.13, 4764.19, 4771.39, 4780.76, 4732.06, 4644.06, 4593.21,
4693.56, 4550.2, 4662.17, 4567.69, 4635.73, 4565.3, 4501.65,
4561.74, 4526.5, 4610.17, 4608.94, 4583.81, 4563.67, 4602.39,
4579.44, 4606.92, 4651.24, 4538.57, 4581.63, 4590.44, 4553.47,
4694.18, 4656.61, 4497.8, 4505.81, 4478.08, 4474.75, 4419.34,
4323.89, 4360.11, 4388.26, 4341.03, 4368.6, 4357.52, 4414.23,
4431.85, 4380.64, 4393.54, 4257.54, 4343.33, 4214.81, 4279.98,
4241.64, 4224.83, 4081.69, 4184.84, 4095.81, 4228.57, 4245.95,
4230.28, 3967.87, 3948.48, 3751.33, 4183.65, 4182.35, 4195.82,
4157.42, 4153.53, 4163.83, 4173.35, 4112.7, 4048.49, 3999.11,
3920.26, 3885.54, 3836.56, 3889.04, 3802.18, 3742.72, 3678.26,
3705.96, 3740.53, 3619.69, 3693.05, 3670, 3654.16, 2739.26,
3651.31, 3624.36, 3550.36, 3501.08, 3576.92, 3498.75, 3348.85,
3368.34, 3319.15, 3281.91, 3107.95, 3135.62, 3033.11, 2825.47,
2860.33, 2764.14, 2476.07, 2039.64, 1724.29, 1555.89, 1424.95}];
lp = ListPlot[elo, Filling -> Axis,
AxesLabel -> {"Network", "Leela Elo"},
AxesStyle -> Arrowheads[{0, 0.02}], PlotRange -> All]
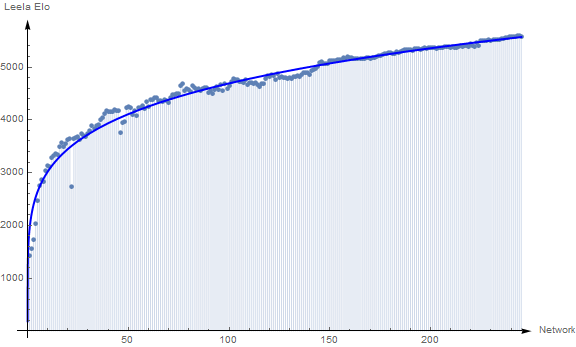
It seems it grows like a powerfunction, so lets check it with WL
data = MapIndexed[{#2[[1]], #1} &, elo];
expr = Normal[NonlinearModelFit[data, b x^a, {a, b}, x]]
1945.17 x^0.191238
This is the powerfunction, now lets visualize it:
pp1 = Plot[expr, {x, 0, Length[elo]},
PlotStyle -> Directive[Blue, Thick], PlotRange -> All];
Show[lp, pp1, PlotRange -> All, AxesOrigin -> {0, 0}]