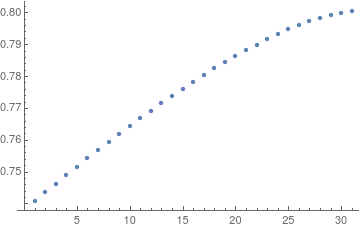
It seems that ArgMin has difficulties for h2 near zero. Also M1 is slow. I would recommend just finding some individual values and using ListPlot, e.g. as below.
pts = Table[M1[h2, alfa], {h2, 1, 4, .1}]
(* During evaluation of In[25]:= FindRoot::lstol: The line search decreased the step size to within tolerance specified by AccuracyGoal and PrecisionGoal but was unable to find a sufficient decrease in the merit function. You may need more than MachinePrecision digits of working precision to meet these tolerances.
Out[25]= {0.740801310481, 0.743546550015, 0.746262102117, \
0.748946758827, 0.751599326706, 0.754218423529, 0.756802639581, \
0.759350378122, 0.761860051955, 0.764329776816, 0.766757576657, \
0.769141333117, 0.77147870336, 0.773767096003, 0.776003732953, \
0.778185434305, 0.780308828275, 0.782370016638, 0.784364756123, \
0.786288212858, 0.788134995015, 0.789898927894, 0.791573003166, \
0.793149155073, 0.794618101184, 0.79596891941, 0.79718881863, \
0.798262566846, 0.799171885286, 0.799894480346, 0.800402813371} *)
ListPlot[pts]