Mathematica gives incorrect answer(A bug !!!), is singular,a MMA has problems to calculate.
(I (MeijerG[{{1/2, 1, 1}, {}}, {{1/2, 1/2, 1}, {}}, -((I Sqrt[a])/b),
1/2] - MeijerG[{{1/2, 1, 1}, {}}, {{1/2, 1/2,
1}, {}}, (I Sqrt[a])/b, 1/2]))/(2 Sqrt[
a] \[Pi]^(3/2) (b + c + I ww)) /. a -> 1 /. b -> 1 /.
c -> 1 /. ww -> 1 // N
(* (0.0179587 + 0.0359174 I) ((-11.1367 - 11.1367 I) +
MeijerG[{{0.5, 1., 1.}, {}}, {{0.5, 0.5, 1.}, {}}, 0. - 1. I, 0.5])*)
Output gives no numeric answer.
intsymbolic = (I (MeijerG[{{1/2, 1, 1}, {}}, {{1/2, 1/2,
1}, {}}, -((I Sqrt[a])/b), 1/2] -
MeijerG[{{1/2, 1, 1}, {}}, {{1/2, 1/2, 1}, {}}, (I Sqrt[a])/b,
1/2]))/(2 Sqrt[a] \[Pi]^(3/2) (b + c + I ww)) /. {a -> 1,
b -> b, c -> 1, ww -> 1};
Plot[Evaluate@ReIm[intsymbolic], {b, 9/10, 11/10}, PlotLegends -> "Expressions"] // Quiet
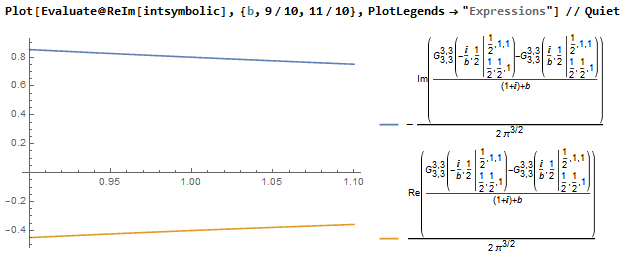
As we can see here on the plot gives incorrect result 0.8 - 0.4 I. A correct answer is:1.395872 - 0.983636 I.
Solution by Maple 2018.
