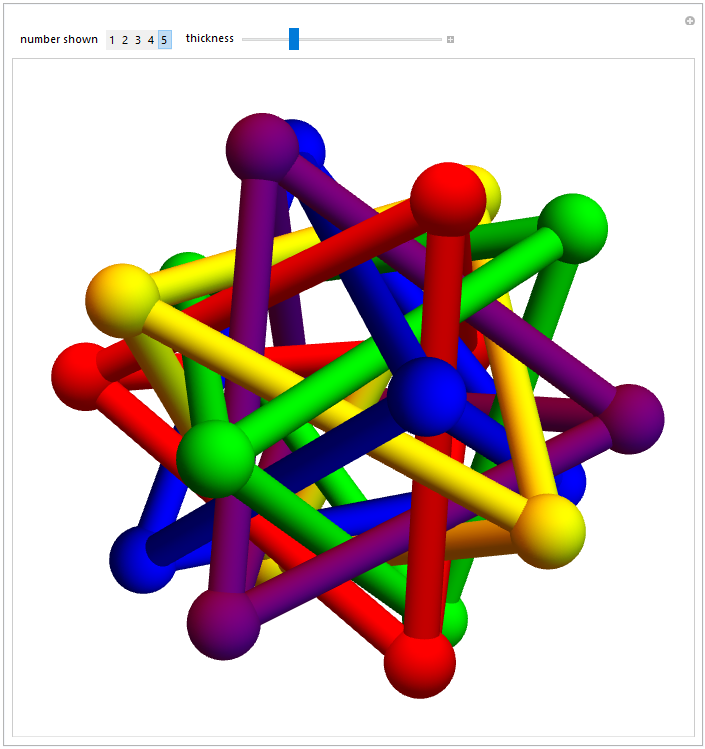
I made a compound of 5 tetrahedra. It's surprisingly sturdy.

This was built with pool noodles. Noodles are 55" (about 4.5 feet) long with a 2 3/8" diameter. Cut in half these give a Length/Diameter ratio of 11.5789. How close is that to a perfect Length/Diameter ratio?

First, lets build up a dodecahedron with simple vertices and an edge length of 1.23607 or $\sqrt5-1$.
From that dodecahedron, find the ten tetrahedra with edge length $2 \sqrt2 $ .
Then find five disjoint tetrahedra. The following code works.
tup=Tuples[{1,-1},{3}];
gold=Table[RotateRight[{0, \[Phi], 1/\[Phi]},n],{n,0,2}];
dodec=RootReduce[Union[Join[tup,Flatten[Table[gold[[n]] tup[[m]],{n,1,3},{m,1,8}],1]]]/.\[Phi]-> GoldenRatio];
tetra=FindClique[Graph[#[[1]]\[UndirectedEdge]#[[2]]&/@Select[Subsets[dodec,{2}],Chop[2 Sqrt[2]-EuclideanDistance@@N[#]]==0&]],{4},All];
compounds=FindClique[Graph[#[[1]]\[UndirectedEdge]#[[2]]&/@Select[Subsets[tetra,{2}],Length[Intersection[#[[1]],#[[2]]]]==0&]],{5},All];
Manipulate[Graphics3D[{
Table[{{Yellow,Red,Green,Purple,Blue}[[n]],Tube[#,thickness]&/@Subsets[compounds[[1,n]],{2}]},{n,1,k}],
Table[{{Yellow,Red,Green,Purple,Blue}[[n]],Sphere[#,thickness 2 ]&/@compounds[[1,n]]},{n,1,k}]}, Boxed-> False, SphericalRegion->True,
ViewAngle-> Pi/10, ImageSize-> 650],
Row[{Control@{{k,5, "number shown"},1,5,1, ControlType->Setter },Spacer[15],
Control@{{thickness,.11, "thickness"},.08,.20,.01, Appearance-> "Labeled" }}], SaveDefinitions->True]
The "perfect" Length/Diameter ratio for rigid tubes seems to be 11.8565. The half-noodle ratio is 11.5789. Since foam is forgiving, I figured that would give a tighter figure, and that turned out to be correct.
For a regular dodecahedron with edge length 1, the inradius and circumradius are 1.11351 and 1.40125.
For an edge length of 1.23607, the inradius and circumradius are 1.37638 and 1.73204.
Based on the sizes of the tetrahedra, we can find the scaling factor of 11.4021.
Height in inches is about 31 inches tall. Distance between vertices is about 14 inches.
The notebook also has a color template. And that's how to build a spikey from pool noodles.
 Attachments:
Attachments: